题目内容
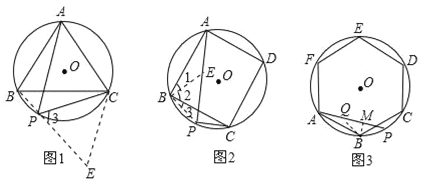
【题目】(1)己知,如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明.
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论不需证明.

【答案】(1)PA=PB+PC;(2)PA=PC+![]() PB;(3)PA=
PB;(3)PA=![]() PB+PC.
PB+PC.
【解析】
试题分析:(1)结论:PA=PB+PC.延长BP至E,使PE=PC,连接CE,证明△PCE是等边三角形.利用CE=PC,∠E=∠3=60°,∠EBC=∠PAC,得到△BEC≌△APC,所以PA=BE=PB+PC;
(2)结论:PA=PC+![]() PB.过点B作BE⊥PB交PA于E,证明△ABE≌△CBP,所以PC=AE,可得PA=PC+
PB.过点B作BE⊥PB交PA于E,证明△ABE≌△CBP,所以PC=AE,可得PA=PC+![]() PB.
PB.
(3)结论:PA=![]() PB+PC.在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=
PB+PC.在AP上截取AQ=PC,连接BQ可证△ABQ≌△CBP,所以BQ=BP.又因为∠APB=30°.所以PQ=![]() PB,PA=PQ+AQ=
PB,PA=PQ+AQ=![]() PB+PC.
PB+PC.
试题解析:
(1)延长BP至E,使PE=PC,连接CE,如图1,∵A、B、P、C四点共圆,∴∠BAC+∠BPC=180°,∵∠BPC+∠EPC=180°,∴∠BAC=∠CPE=60°,PE=PC,∴△PCE是等边三角形,∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP,∵△ABC、△ECP为等边三角形,∴CE=PC,AC=BC,在△BEC和△APC中,∵CE=PC,∠BEC=∠ACP,BC=AC,∴△BEC≌△APC(SAS),∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,如图2,∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,∴∠APB=45°,∴BP=BE,∴PE=![]() PB,在△ABE和△CBP中,∵BE=BP,∠1=∠3,AB=BC,∴△ABE≌△CBP(SAS),∴PC=AE,∴PA=AE+PE=PC+
PB,在△ABE和△CBP中,∵BE=BP,∠1=∠3,AB=BC,∴△ABE≌△CBP(SAS),∴PC=AE,∴PA=AE+PE=PC+![]() PB;
PB;
(3)PA=PC+![]() PB.
PB.
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,连接BQ,如图3,∵∠BAP=∠BCP,AB=BC,在△ABQ和△CBP中,∵AQ=PC,∠BAP=∠BCP,AB=BC,∴△ABQ≌△CBP(SAS),∴BQ=BP,∴MP=QM,又∵∠APB=30°,∴cos30°=![]() ,∴PM=
,∴PM=![]() PB,∴PQ=
PB,∴PQ=![]() PB,∴PA=PQ+AQ=PC+
PB,∴PA=PQ+AQ=PC+![]() PB.
PB.

【题目】某学习小组9名学生参加“数学竞赛”,他们的得分情况如表:
人数(人) | 1 | 3 | 4 | 1 |
分数(分) | 80 | 85 | 90 | 95 |
那么这9名学生所得分数的众数和中位数分别是( )
A.90,90
B.90,85
C.90,87.5
D.85,85