题目内容
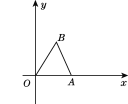
【题目】如图，在直角坐标系中，已知点A(6，0)，又点B(x，y)在第一象限内，且x＋y＝8，设△AOB的面积是S.
(1)写出S与x之间的函数解析式，并求出x的取值范围；
(2)画出(1)中所求函数的图象．
【答案】（1）0＜x＜8.（2）详见解析.
【解析】
（1）根据点A、B的坐标求得△AOB的底边OA与高线BC的长度；然后根据三角形的面积公式即可求得S与x的函数关系式；
（2）利用“两点确定一条直线”来画一次函数的图象；
（1）∵点B在直线y=-x+8上，∴设B（x，-x+8），
∴y=-x+8与x和y轴的交点分别为（8，0）和（0，8）∵点B在第一象限，∴其横坐标x的范围是：0＜x＜8；
∵A（6，0），点B（x，y），
∴OA=6，BC=y（y＞0），
∴S=
OABC=×6y=3y；
又∵x+y=8，
∴y=8-x，
∴S=-3x+24.
由
，
解得0＜x＜8.
(2) ∵由（1）知，S=-3x+24（0＜x＜8）；
令S=0，则x=8；
令x=0，则S=24，
∴一次函数S=-3x+24（x＞0）经过点（8，0）、（0，24），
∴其图象如图所示：
练习册系列答案
全能测控期末小状元系列答案
相关题目
