题目内容
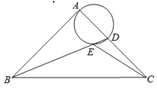
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC,BC=2![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A. 3 B. 1 C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AE,如图1,先根据等腰三角形的性质得到AB=AC=2,再根据圆周角定理,由AD为直径得到∠AED=90°,接着由∠AEB=90°得到点E在以AB为直径的⊙O上,于是当点O、E、C共线时,CE最小,如图2,在Rt△AOC中利用勾股定理计算出OC,从而得到CE的最小值.
连接AE,如图1,
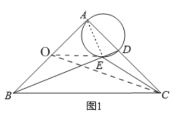
∵∠BAC=90°,AB=AC,BC=2![]() ,∴AB=AC=2,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的⊙O上,∵⊙O的半径为1,连接OE,OC,∴OE=
,∴AB=AC=2,∵AD为直径,∴∠AED=90°,∴∠AEB=90°,∴点E在以AB为直径的⊙O上,∵⊙O的半径为1,连接OE,OC,∴OE=![]() AB=1,在Rt△AOC中,∵OA=2,AC=4,∴OC=
AB=1,在Rt△AOC中,∵OA=2,AC=4,∴OC=![]() =
=![]() ,由于OC=
,由于OC=![]() ,OE=1是定值,点E在线段OC上时,CE最小,如图2,
,OE=1是定值,点E在线段OC上时,CE最小,如图2,
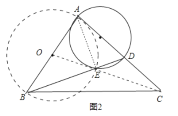
∴CE=OC-OE=![]() -1,即线段CE长度的最小值为
-1,即线段CE长度的最小值为![]() -1,故答案选D.
-1,故答案选D.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目