Question

【题目】如图，点P为反比例函数y=（x＞0）图象上一点，以点P为圆心作圆，且该圆恰与两坐标轴都相切．在y轴任取一点E，连接PE并过点P作直线PE的垂线与x轴交于点F，则线段OE与线段OF的长度可能满足的数量关系式是 ．

Answer 1

【答案】OF﹣OE=2或OE﹣OF=2或OF+OE=2．

【解析】

试题分析：设以P为圆心的⊙P与两坐标轴相切的切点分别为B，A，如图，连接PB,PA，

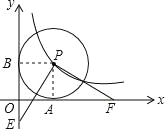
利用P点在双曲线y=（x＞0）图象上且以P为圆心的⊙P与两坐标轴都相切，求出P点坐标，再利用△BPE≌△APF，分三种情况列出OE与OF之间的关系．∵点P在双曲线y=（x＞0）上，以P为圆心的⊙P与两坐标轴都相切，PB=PA，∴P（1，1），又∵PF⊥PE，∴∠EPF=90°，∵∠BPE+∠EPA=90°，∵∠EPA+∠FPA=90°，∴∠FPA=∠BPE，在△BPE和△APF中，∴△BPE≌△APF，∴AF=BE.①当F在x轴的正半轴，且OF＞1时，则有OF﹣OA=OB+OE，即OF﹣1=1+OE，∴OF﹣OE=2；②当F在x轴的负半轴时，则有OF+OA=OE﹣OB，即OF+1=OE﹣1，∴OE﹣OF=2；③当F在x轴的正半轴，且OF＜1时，则有OA﹣OF=OE﹣OB，即1﹣OF=OE﹣1，∴OF+OE=2，综上，线段OE与线段OF的长度可能满足的数量关系式是：OF﹣OE=2或OE﹣OF=2或OF+OE=2，故答案为：OF﹣OE=2或OE﹣OF=2或OF+OE=2．