题目内容
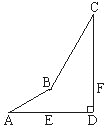
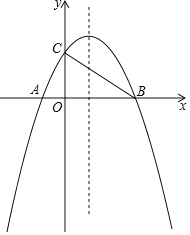
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q 作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR是以PQ为一腰的等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由
【答案】(1)![]() ;
;
(2)![]() .
.
(3)当![]() 为
为![]() 或6或
或6或![]() 时,△PQR为等腰三角形.
时,△PQR为等腰三角形.
【解析】
(1)根据△RQC∽△ABC,根据相似三角形的对应边成比例可求解DH;
(2)根据三角形的相似比求出y关于x的函数关系式;
(3)画出图形,根据图形进行讨论:
① 当PQ=PR时,过点P作PM⊥QR于M,则QM=RM.由于∠1+∠2=90°,∠C+∠2=90°,∴∠1=∠C.
∴cos∠1=cosC=![]() =
=![]() ,∴
,∴![]() ,即可求出x的值;
,即可求出x的值;
② 当PQ=RQ时,-![]() x+6=
x+6=![]() ,x=6;
,x=6;
③当PR=QR时,则R为PQ中垂线上的点,于是点R为EC的中点,故CR=![]() CE=
CE=![]() AC=2.
AC=2.
(1)![]() ,AB=6,AC=8,
,AB=6,AC=8,![]() .
.
![]() 点D为AB中点,
点D为AB中点,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
∴![]() ,
,
(2)![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() 关于
关于![]() 的函数关系式为:
的函数关系式为:![]() .
.
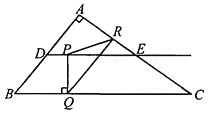
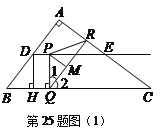
(3)存在,分三种情况:
①如图(1),当![]() 时,过点P作
时,过点P作![]() 于M,则
于M,则![]() .
.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
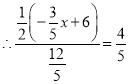 ,
,
![]() .
.
②如图(2),当![]() 时,
时,
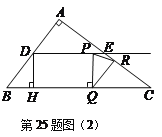
![]() ,
,
![]() .
.
③如图(3),当![]() 时,则R为PQ中垂线上的点,于是点R为EC的中点,
时,则R为PQ中垂线上的点,于是点R为EC的中点,
![]() .
.
![]() ,
,
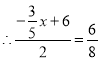 ,
,
![]() .
.
综上所述,当![]() 为
为![]() 或6或
或6或![]() 时,△PQR为等腰三角形.
时,△PQR为等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】现有![]() 、
、![]() 型两种客车,它们的载客量和租金如下表:
型两种客车,它们的载客量和租金如下表:
|
| |
载客量/(人/辆) |
|
|
租金/(元/辆) |
|
|
某学校计划在总费用![]() 元的限额内,租用
元的限额内,租用![]() 、
、![]() 型客车共5辆送九年级师生集体外出活动.
型客车共5辆送九年级师生集体外出活动.
(Ⅰ)设租用![]() 型客车
型客车![]() 辆(
辆(![]() 为非负整数),根据题意,用含
为非负整数),根据题意,用含![]() 的式子填写下表:
的式子填写下表:
车辆数/辆 | 载客量 | 租金/元 | |
|
|
|
|
|
|
(Ⅱ)若九年级师生共有![]() 人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.
人,请给出能完成此项任务的最节省费用的租车方案,并说明理由.