题目内容
【题目】探索
(x-1)(x+1)=x2-1
(x-1)(x2+x+1)=x3-1
(x-1)(x2+x2+x+1)=x4-1
(x-1)(x4+x3+x2+x+1)=x5-1
(1)试写出第七个等式;
(2)试求26+25+24+23+22+2+1的值;
(3)判断22018+22017+22016+22015…+22+2+1的值的个位数字是几.
【答案】(1)![]() ;(2)127;(3)7
;(2)127;(3)7
【解析】
(1)根据规律题中的已知条件得到规律即可求出第七个等式;
(2)将x=2代入代数式,且依据等式的规律列式即可计算得出答案;
(3)先计算该代数式的值得到结果为![]() ,再探究得到个位数字的规律即可得到答案.
,再探究得到个位数字的规律即可得到答案.
解:(1)第七个等式:![]() .
.
(2)原式![]() ,
,
![]() ,
,
![]() ;
;
(3)原式![]()
![]() ,
,
因为:![]() 的个位数字是1,
的个位数字是1,![]() 的个位数字是3,
的个位数字是3,![]() 的个位数字是7.
的个位数字是7.![]() 的个位数字是5,
的个位数字是5,![]() 的个位数字是1…所以
的个位数字是1…所以![]() 的个位数字是7.
的个位数字是7.

练习册系列答案
相关题目
【题目】如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
坡度 | 1:20 | 1:16 | 1:12 |
最大高度(米) | 1.50 | 1.00 | 0.75 |
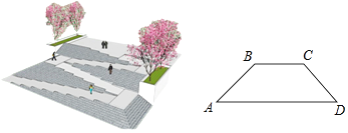
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.





