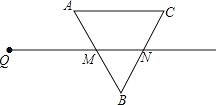题目内容
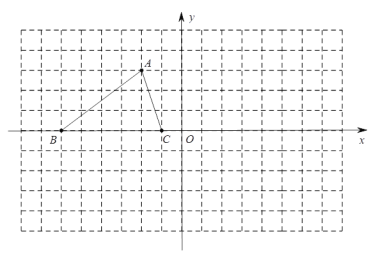
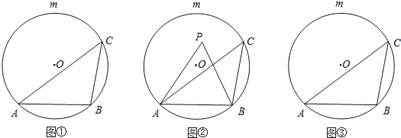
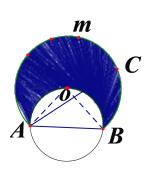
【题目】如图①,AB是圆O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)若∠ACB=45°,点P是O上一点(不与A.B重合),则∠APB=___;
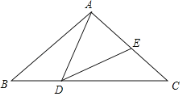
(2)如图②,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
(3)请在图③中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足
所围成的弓形区域内满足
![]() 的点P所在的范围;
的点P所在的范围;
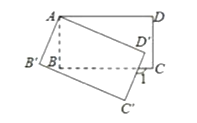
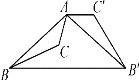
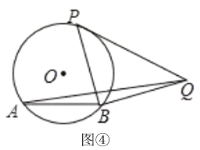
(4)在(1)的条件下,以PB为边,向右作等腰直角三角形PBQ,连结AQ,如图4,已知AB=2,
①当点Q在线段AB的延长线上时,线段AQ的长为____________
②线段AQ的最小值为_____________
【答案】(1)45°或135°;(2)答案见详解;(3)答案见详解;(4)① 4;②![]()
【解析】
(1)根据题意,点P在优弧![]() 上时,∠APB=∠ACB=45°;当点P在劣弧
上时,∠APB=∠ACB=45°;当点P在劣弧![]() 上时,∠APB=180°-∠ACB=135°;
上时,∠APB=180°-∠ACB=135°;
(2)延长AP交圆O于点Q,连接BQ,根据三角形的外角大于任何一个与它不相邻的内角,可以得证;
(3)根据第(2)问和圆周角定理可知,画出过点A、B、O的圆,即可得到点P所在的阴影部分;
(4)①根据题意可知,![]() 是等腰直角三角形,点Q在线段AB的延长线上时,点P只能在优弧
是等腰直角三角形,点Q在线段AB的延长线上时,点P只能在优弧![]() 上,且
上,且![]() ,证明
,证明![]() 是等腰直角三角形即可得解;
是等腰直角三角形即可得解;
②根据题意,连接PA,设PQ交![]() 于点T,连接AT,BT,可得AT是
于点T,连接AT,BT,可得AT是 ![]() 的直径,即
的直径,即![]() 是等腰直角三角形,AB=BT=2,以BT为底向右作等腰RtBKT,则KT=KB=
是等腰直角三角形,AB=BT=2,以BT为底向右作等腰RtBKT,则KT=KB=![]() ,由∠BQT=45°,可得点Q的运动轨迹是以K为圆心,KT为半径的圆;求出AK的值为
,由∠BQT=45°,可得点Q的运动轨迹是以K为圆心,KT为半径的圆;求出AK的值为![]() ,最后根据三角形三边长的关系,即可得到AQ的最小值.
,最后根据三角形三边长的关系,即可得到AQ的最小值.
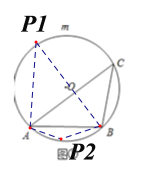
(1)如图①所示,
第一种情况:点P在优弧![]() 上时,∠AP1B=∠ACB=45°;
上时,∠AP1B=∠ACB=45°;
第二种情况:点P在劣弧![]() 上时,
上时,
∵四边形ACBP2是圆的内接四边形,
∴![]()
∴∠AP2B=180°-∠ACB=135°,
故答案为:45°或135°;
(2)如图②所示,延长AP交圆O于点Q,连接BQ,则![]() ,
,
∵![]()
∴∠APB>∠PQB,即∠APB>∠ACB;

(3)连接AO,BO,作![]() 的外接圆,即可得到所求的阴影部分;
的外接圆,即可得到所求的阴影部分;
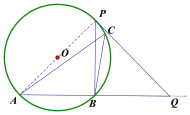
(4)①如图:
∵![]() 是等腰直角三角形,点Q在线段AB的延长线上,
是等腰直角三角形,点Q在线段AB的延长线上,
∴点P只能在优弧![]() 上,且
上,且![]() ,
,
连接AP,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ;
;
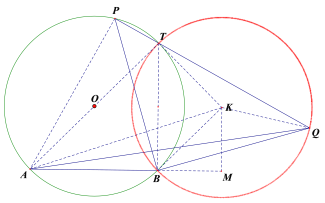
②如图,连接PA,设PQ交![]() 于点T,连接AT,BT.
于点T,连接AT,BT.
∵∠APB=∠BPQ=45°,
∴∠APT=90°,
∵∠TAB=∠BPQ=45°,∠ABT=90°,
∴AB=BT=2,
以BT为底边向右作等腰RtBKT,则KT=KB=![]() ,
,
∵∠BQT=45°,
∴点Q的运动轨迹是以K为圆心,KT为半径的圆,KQ=KT=KB=![]()
作KM⊥BA交AB的延长线于点M,连接AK,MB=KM=1,AM=3,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AQ的最小值是![]() .
.

 名校课堂系列答案
名校课堂系列答案