��Ŀ����
����Ŀ����������c1�� ![]() ��x�ᷭ�ۣ��õ�������c2 �� ��ͼ1��ʾ��
��x�ᷭ�ۣ��õ�������c2 �� ��ͼ1��ʾ��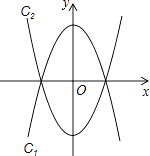
��1����ֱ��д��������c2�ı���ʽ��
��2���ֽ�������c1����ƽ��m����λ���ȣ�ƽ�ƺ�õ��������ߵĶ���ΪM����x��Ľ������������ΪA��B����������c2����Ҳƽ��m����λ���ȣ�ƽ�ƺ�õ��������ߵĶ���ΪN����x��Ľ������������ΪD��E��
�ٵ�B��D���߶�AE�����ȷֵ�ʱ����m��ֵ������ƽ�ƹ����У��Ƿ�����Ե�A��N��E��MΪ������ı����Ǿ��ε����Σ������ڣ��������ʱm��ֵ���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺y= ![]() x2��
x2�� ![]()
��2��
�⣺����ͼ1��� ![]() x2+
x2+ ![]() =0����x1=��1��x2=1
=0����x1=��1��x2=1
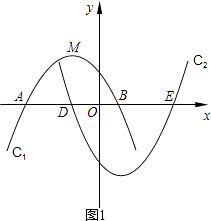
������c1��x�������������������1��0������1��0����
��A����1��m��0����B��1��m��0����
ͬ���ɵã�D����1+m��0����E��1+m��0����
��AD= ![]() AEʱ��
AEʱ��
����1+m��������1��m��= ![]() [��1+m��������1��m��]��
[��1+m��������1��m��]��
��m= ![]() ��
��
��BD= ![]() AEʱ��
AEʱ��
����1+m������1��m��= ![]() [��1+m��������1��m��]��
[��1+m��������1��m��]��
��m=2��
�ʵ�B��D���߶�AE�����ȷֵ�ʱ��m= ![]() ��2��
��2��
�ڴ��ڣ�
���ɣ���ͼ2������AN��NE��EM��MA��

������ɵã�M����m�� ![]() ����N��m����
����N��m���� ![]() ����
����
��M��N����ԭ��O�Գƣ�
��OM=ON��
��A����1��m��0����E��1+m��0����
��A��E����ԭ��O�Գƣ�
��OA=OE
���ı���ANEMΪƽ���ı��Σ�
��AM2=����m+1+m��2+�� ![]() ��2=4��
��2=4��
ME2=��1+m+m��2+�� ![]() ��2=4m2+4m+4��
��2=4m2+4m+4��
AE2=��1+m+1+m��2=4m2+8m+4��
��AM2+ME2=AE2����4+4m2+4m+4=4m2+8m+4��
��m=1��
��ʱ��AME��ֱ�������Σ��ҡ�AME=90�㣮
�൱m=1ʱ���Ե�A��N��E��MΪ������ı����Ǿ��Σ�
����������1�����ݷ��۵����ʿ�������c2�ı���ʽ����2�������������c1��x��������������꣬�ֵ�AD= ![]() AEʱ����BD=
AEʱ����BD= ![]() AEʱ�������������⣻�ڴ��ڣ����ɣ���ͼ2������AN��NE��EM��MA�����ݾ��ε��ж����ɵó���
AEʱ�������������⣻�ڴ��ڣ����ɣ���ͼ2������AN��NE��EM��MA�����ݾ��ε��ж����ɵó���
�����㾫����������Ŀ����֪���������ö��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��