题目内容
【题目】在△ABC中，AB＝AC
（1）利用直尺和圆规完成如下操作，作∠BAC的平分线和AB的垂直平分线，交点为P（不写作法，保留作图瘕迹）
（2）连结PB，若∠ABC＝65°，求∠ABP的度数．
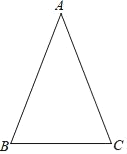
【答案】（1）如图，点P为所作；见解析；（2）∠ABP＝25°．
【解析】
（1）利用基本作图，作AB的垂直平分线和∠BAC的平分线得到P点；
（2）AD为∠BAC的平分线，如图，利用等腰三角形的性质得AD⊥BC，再利用PA＝PB得到∠ABP＝∠BAP，然后利用互余计算出∠BAD＝25°，从而得到∠ABP的度数．
（1）如图，点P为所作；
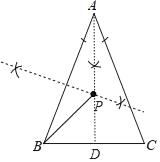
（2）AD为∠BAC的平分线，如图，
∵AB＝AC，
∴AD⊥BC，
∵点P在AB的垂直平分线上，
∵PA＝PB，
∴∠ABP＝∠BAP，
∵∠ABD+∠BAD＝90°，
∴∠BAD＝90°﹣65°＝25°，
∴∠ABP＝25°．
名师金手指领衔课时系列答案【题目】如图，点P是
上一动点，连接AP，作∠APC=45°，交弦AB于点C．AB=6cm．
小元根据学习函数的经验，分别对线段AP，PC，AC的长度进行了测量．
下面是小元的探究过程，请补充完整：
（1）下表是点P是上的不同位置，画图、测量，得到线段AP，PC，AC长度的几组值，如下表：
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 （保留一位小数）．
②在AP，PC，AC的长度这三个量中，确定
的长度是自变量，的长度和 的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数图象；
（3）结合函数图象，解决问题：当△ACP为等腰三角形时，AP的长度约为 cm（保留一位小数）．
【题目】为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
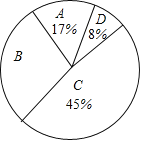
请根据所给信息，解答以下问题：
(1)表中a=___，b=___；
(2)请计算扇形统计图中B组对应扇形的圆心角的度数；
(3)已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率。
【题目】在生活中，有很多函数并不一定存在解析式，对于这样的函数，我们可以通过列表和图象来对它可能存在的性质进行探索，例如下面这样一个问题：
已知y是x的函数，下表是y与x的几组对应值．
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 1.969 | 1.938 | 1.875 | 1.75 | 1 | 0 | ﹣2 | ﹣1.5 | 0 | 2.5 | … |
小孙同学根据学习函数的经验，利用上述表格反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．
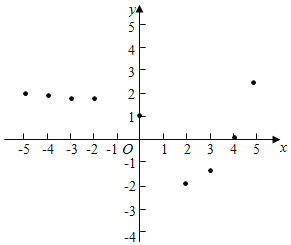
下面是小孙同学的探究过程，请补充完整；
（1）如图，在平面之间坐标系xOy中，描出了以上表中各对应值为坐标的点，根据描出的点，画出函数的图象：
（2）根据画出的函数图象回答：
①x＝﹣1时，对应的函数值y的为 ；
②若函数值y＞0，则x的取值范围是 ；
③写出该函数的一条性质（不能与前面已有的重复）： ．