题目内容
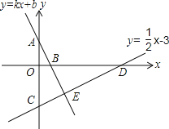
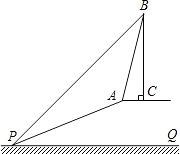
【题目】如图所示,直线 y=x+2 与两坐标轴分别交于A、B 两点,点 C 是 OB 的中点,D、E 分 别是直线 AB、y 轴上的动点,则△CDE 周长的最小值是________.
【答案】![]()
【解析】
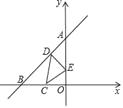
先求出A,B两点坐标,得到C点坐标,然后分别求出C点关于直线AB与y轴的对称点C′和C′′的坐标,连接C′,C′′,交AB和y轴的于点D,E,此时△CDE的周长最小,求出线段C′C′′的长即可.
解: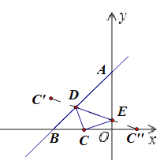
由题意可知A(0,2),B(﹣2,0),
∵点 C 是 OB 的中点,
∴C(﹣1,0),
如图,点C关于直线AB的对称点C′(﹣2,1),点C关于y轴的对称点C′′(1,0),
连接C′C′′与AB交于D点,与AO交于E点,此时△CDE的周长最小,
△CDE周长=CD+DE+CE=DC′+DE+EC″= C′C″=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目