题目内容
在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有_________条.
3.
解析试题分析:如图,易知,
当PD∥BC时,△APD∽△ABC.
当PE∥AC时,△PBE∽A△BC.
连接PC,
∵∠A=36°,AB=AC,点P在AC的垂直平分线上,
∴AP=PC,∠ABC=∠ACB="72°." ∴∠ACP=∠PAC="36°." ∴∠PCB=36°.
∴∠B=∠B,∠PCB=∠A,∴△CBP∽△ABC.
∴过点P的△ABC的相似线最多有3条.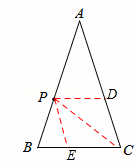
考点:1.新定义;2.单动点问题;3.线段垂直平分线的性质;4.等腰三角形的性质;5.三角形内角和定理;6.相似三角形的判定;7.分类思想的应用.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
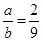 ,则
,则 ___________.
___________.
 .
.
 (x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为__________.
(x>0)的图象分别交于点B1,B2,B3,分别过点B1,B2,B3作x轴的平行线,分别与y轴交于点C1,C2,C3,连接OB1,OB2,OB3,那么图中阴影部分的面积之和为__________.
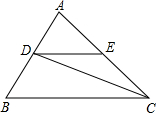
 中,点
中,点 、
、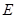 分别在边
分别在边 、
、 上,
上, 平分
平分 ,
,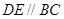 ,如果
,如果 ,
, ,那么
,那么 .
.
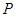 是线段
是线段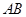 的黄金分割点,
的黄金分割点,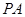 >
>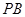 ,且
,且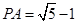 ,则
,则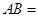 .
.