题目内容
【题目】如图,在△ABC中,AB=AC,E在AC上,且AD=AE,DE的延长线与BC相交于点F.求证:DF⊥BC. 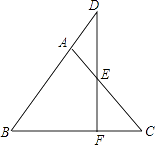
【答案】证明:如图,过A作AM⊥BC于M,
∵AB=AC,
∴∠BAC=2∠BAM,
∵AD=AE,
∴∠D=∠AED,
∴∠BAC=∠D+∠AED=2∠D,
∴∠BAC=2∠BAM=2∠D,
∴∠BAM=∠D,
∴DF∥AM,
∵AM⊥BC,
∴DF⊥BC.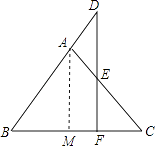
【解析】过A作AM⊥BC于M,根据等腰三角形三线合一的性质得出∠BAC=2∠BAM,由三角形外角的性质及等边对等角的性质得出∠BAC=2∠D,则∠BAM=∠D,根据平行线的判定得出DF∥AM,进而得到DF⊥BC.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

练习册系列答案
相关题目