题目内容
小明在探究性学习中认为:“分式的基本性质虽然没有如下结论:| a |
| b |
| a+m |
| b+m |
请你先分别解两个方程:
| 60 |
| x |
| 60+7 |
| x+7 |
| 30 |
| x |
| 30-4 |
| x-4 |
| a |
| b |
| a+m |
| b+m |
分析:观察可得最简公分母,方程两边乘最简公分母,可以把分式方程转化为整式方程求解.再根据这两个方程的解得出
=
(b≠0,b+m≠0,m≠0)成立时a、b的关系.
| a |
| b |
| a+m |
| b+m |
解答:解:
=
方程的两边同乘x(x+7),得
60x+420=67x,
解得x=60.
检验:把x=60代入x(x+7)≠0.
∴原方程的解为:x=60.
=
,
方程的两边同乘x(x-4),得
30x-120=26x,
解得x=30.
检验:把x=30代入x(x-4)≠0.
∴原方程的解为:x=30.
∴两个方程分别得:x=60,x=30.
猜想得:“当a=b时,
=
成立.”
| 60 |
| x |
| 60+7 |
| x+7 |
方程的两边同乘x(x+7),得
60x+420=67x,
解得x=60.
检验:把x=60代入x(x+7)≠0.
∴原方程的解为:x=60.
| 30 |
| x |
| 30-4 |
| x-4 |
方程的两边同乘x(x-4),得
30x-120=26x,
解得x=30.
检验:把x=30代入x(x-4)≠0.
∴原方程的解为:x=30.
∴两个方程分别得:x=60,x=30.
猜想得:“当a=b时,
| a |
| b |
| a+m |
| b+m |
点评:本题考查了分式方程的解法,(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
(2)解分式方程一定注意要验根.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 (b≠0,b+m≠0,m≠0),但当a、b满足某种关系时,该结论会成立.”
(b≠0,b+m≠0,m≠0),但当a、b满足某种关系时,该结论会成立.”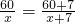 与
与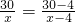 ,再猜想:当a、b满足什么关系时,
,再猜想:当a、b满足什么关系时, (b≠0,b+m≠0,m≠0),但当a、b满足某种关系时,该结论会成立.”
(b≠0,b+m≠0,m≠0),但当a、b满足某种关系时,该结论会成立.” 与
与 ,再猜想:当a、b满足什么关系时,
,再猜想:当a、b满足什么关系时, (b≠0,b+m≠0,m≠0)成立.
(b≠0,b+m≠0,m≠0)成立.