题目内容
“数缺形时少直观,形少数时难入微”,小明在探究| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
(1)则可以得出线段C1B=
(2)从而发现了
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
(3)小明学习上爱动脑,经过认真思考和分析后,发现在计算
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n |
请你对小明的发现,试给出必要的说理.
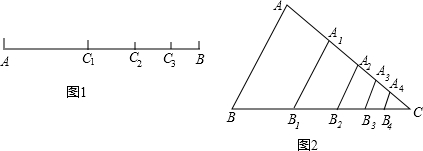
分析:(1)根据线段中点的定义写出前两个,并发现后一段是前一段的
,然后求出Cn-1Cn=CnB,ACn=AB-CnB,代入数即可;
(2)与线段联系发现,这列数据的和等于线段AB,所以这列数的和等于1;
(3)根据三角形的中位线定理与相似三角形的面积的比等于相似比的平方可得这列数分别是被依次分割取得的三角形的面积,根据三角形的面积分别表示出四边形ABB1A1的面积,四边形A1B1B2A2的面积,四边形A2B2B3A3的面积,…四边形An-1Bn-1BnAn的面积,再根据所有四边形的面积相加即可得解.
| 1 |
| 2 |
(2)与线段联系发现,这列数据的和等于线段AB,所以这列数的和等于1;
(3)根据三角形的中位线定理与相似三角形的面积的比等于相似比的平方可得这列数分别是被依次分割取得的三角形的面积,根据三角形的面积分别表示出四边形ABB1A1的面积,四边形A1B1B2A2的面积,四边形A2B2B3A3的面积,…四边形An-1Bn-1BnAn的面积,再根据所有四边形的面积相加即可得解.
解答:解:(1)∵AB=1,C1为AB的中点,
∴C1B=
AB=
,
∵C2为C1B的中点,
∴C1C2=
C1B=
×
=
,
以此类推,每取一次中点,线段的长度变为前一次的
,
∴Cn-1Cn=CnB=(
)n=
,
∴ACn=AC-CnB=1-
;
(2)结合图形,
+
+…+
+
=AC1+C1C2+…+CnB=ACn,
∴
+
+…+
+
=1-
;
(3)∵正△ABC面积为1,A1、B1分别为AC、BC两边的中点,
∴S△A1B1C=
S△ABC=
,
∴S四边形ABB1A1=3S△A1B1C=3×
,
同理S△A2B2C=
S△A1B1C=
×
=
,
∴S四边形A1B1B2A2=3S△A2B2C=3×
,
…
以此类推S四边形An-1Bn-1BnAn=3S△AnBnC=3×
,
S△AnBnC=
,
∵S△ABC=S四边形ABB1A1+S四边形A1B1B2A2+…+S四边形An-1Bn-1BnAn+S△AnBnC=1,
即3×
+3×
+…+3×
+
=1,
∴
+
+…+
=
.
故答案为:(1)
,
,1-
;(2)1;(3)
.
∴C1B=
| 1 |
| 2 |
| 1 |
| 2 |
∵C2为C1B的中点,
∴C1C2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
以此类推,每取一次中点,线段的长度变为前一次的
| 1 |
| 2 |
∴Cn-1Cn=CnB=(
| 1 |
| 2 |
| 1 |
| 2n |
∴ACn=AC-CnB=1-
| 1 |
| 2n |
(2)结合图形,
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
∴
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| 1 |
| 2n |
| 1 |
| 2n |
(3)∵正△ABC面积为1,A1、B1分别为AC、BC两边的中点,
∴S△A1B1C=
| 1 |
| 4 |
| 1 |
| 4 |
∴S四边形ABB1A1=3S△A1B1C=3×
| 1 |
| 4 |
同理S△A2B2C=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 42 |
∴S四边形A1B1B2A2=3S△A2B2C=3×
| 1 |
| 42 |
…
以此类推S四边形An-1Bn-1BnAn=3S△AnBnC=3×
| 1 |
| 4n |
S△AnBnC=
| 1 |
| 4n |
∵S△ABC=S四边形ABB1A1+S四边形A1B1B2A2+…+S四边形An-1Bn-1BnAn+S△AnBnC=1,
即3×
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 4n |
| 1 |
| 4n |
∴
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 4n |
1-
| ||
| 3 |
故答案为:(1)
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
1-
| ||
| 3 |
点评:本题是对图形变化问题的考查,把数据融合与图形的线段的长度或面积中,做到数形结合,用图形表示数据,用数据描述图形是解题的关键,也是解题的突破口,本题难度较大,灵活性较强,求解时一定要小心仔细.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 并利用图形做必要的推理说明)
并利用图形做必要的推理说明)