题目内容
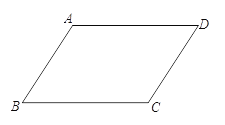
【题目】如图,在直角梯形 ABCD 中,AD∥BC,∠ABC=90°,AB=7,AD=3, BC=4.点 P 为 AB 边上一动点,若△PAD 与△PBC 是相似三角形,则满足条件的点 P 的个数是( )
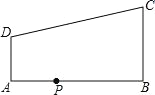
A. 1个 B. 2 个 C. 3 个 D. 4 个
【答案】B
【解析】
由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况
讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出 AP 的长,即可得到 P 点的个数.
∵AB⊥BC,
∴∠B=90°,
∵AD∥BC,
∴∠A=180°﹣∠B=90°,
∴∠PAD=∠PBC=90°,
设AP的长为x,则BP长为7﹣x;
若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:
①若△APD∽△BPC,则 AP:BP=AD:BC, 即 x:(7﹣x)=3:4,
解得:x=3
②若△APD∽△BCP,则 AP:BC=AD:BP, 即 x:4=3:(7﹣x),
解得:x=4或3.
∴满足条件的点 P 的个数是 2个,
故选:B.

【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售价 x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
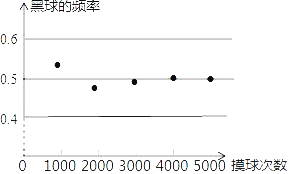
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
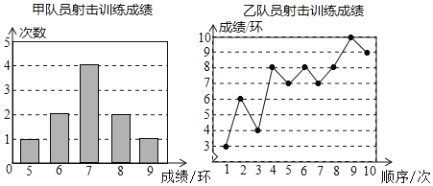
根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员.
【题目】物理兴趣小组![]() 位同学在实验操作中的得分情况如下表:
位同学在实验操作中的得分情况如下表:
得分(分) |
|
|
|
|
人数(人) |
|
|
|
|
问:(1)这![]() 位同学实验操作得分的众数是 ,中位数是
位同学实验操作得分的众数是 ,中位数是
(2)这![]() 位同学实验操作得分的平均分是多少?
位同学实验操作得分的平均分是多少?
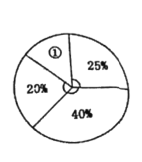
(3)将此次操作得分按人数制成如图所示的扇形统计图.扇形①的圆心角度数是多少?