题目内容
【题目】已知∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.
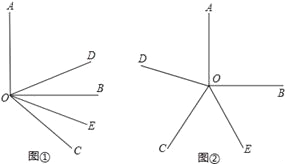
(1)如图①,当∠BOC=70°时,求∠DOE的度数;
(2)如图②,当射线OC在∠AOB内绕O点旋转时,∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数;
(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,判断∠DOE的大小是否发生变化若变化,说明理由;若不变,求∠DOE的度数.

【答案】(1)∠DOE=45°;(2)∠DOE的大小不变等于45°.理由见解析;(3)∠DOE的大小发生变化,∠DOE=45°或135.
【解析】试题分析:(1)根据角平分线的定义,OD、OE分别平分∠AOC和∠BOC,则可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)结合角的特点,∠DOE=∠DOC+∠COE,求得结果进行判断和计算;
(3)正确作出图形,判断大小变化.
试题解析:
解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE=![]() ∠COB=35°,∠COD=
∠COB=35°,∠COD=![]() ∠AOC=10°,
∠AOC=10°,
∴∠DOE=45°;
(2)∠DOE的大小不变等于45°.
理由:∠DOE=∠DOC+∠COE=![]() ∠COB+
∠COB+![]() ∠AOC
∠AOC
=![]() (∠COB+∠AOC)
(∠COB+∠AOC)
=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小发生变化,∠DOE=45°或135.
如图①,∠DOE=45°;
如图②,∠DOE=135°.(说理过程同(2))
点睛: 此题主要考查了角平分线的性质以及角的有关计算,正确作图,熟记角的特点与角平分线的定义是解决此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

