��Ŀ����
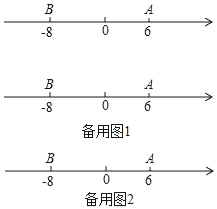
����Ŀ����֪����������A��B��Ӧ�����ֱ���6����8��M��N��PΪ�������������㣬��M��A������ٶ�Ϊÿ��2����λ���ȣ���N�ӵ�B�����ٶ�Ϊ��M��3������P��ԭ������ٶ�Ϊÿ��1����λ���ȣ�
��1����A��B����ľ���Ϊ�� ������λ���ȣ�
��2������M�����˶���ͬʱ��N�����˶������ʱ���M���N���54����λ���ȣ�
��3������M��N��Pͬʱ�������˶�������M���N������M��P������ԭ�����ٶ������˶�����N�ı��˶�������ԭ�����ٶ������˶�����ӿ�ʼ�˶������ʱ���P����M��N�ľ�����ȣ�
���𰸡���1��14����2��5�룻��3��![]() ���3.5���
���3.5���![]() ��.
��.
��������
��1�����������ľ��빫ʽ�������A��B����ľ��룻
��2���辭��x���M���N���54����λ���ɵ�M��A������ٶ�Ϊÿ��2����λ����N�ӵ�B�����ٶ�ΪM���3�����ó�2x+6x+14��54������ɣ�
��3�����������M���N������ʱ��Ϊ14�£�6��2����3.5�룬��ʱN���Ӧ�����ǩ�8+6��3.5��13������ӿ�ʼ�˶�������ǰ����t���P����M��N�ľ�����ȣ���������t���P����M��N�ľ�����ȣ�����PM��PN�г����̣�������⼴�ɣ�
�⣺��1��������������A��B��Ӧ�����ֱ���6����8��
��A��B����ľ���Ϊ6������8����14��
�ʴ�Ϊ14��
��2���辭��x���M���N���54����λ��
��������з���Ϊ��2x+6x+14��54��
�ⷽ�̣���x��5��
�𣺾���5���M���N���54����λ��
��3����M���N������ʱ��Ϊ14�£�6��2����3.5�룬
��ʱN���Ӧ�����ǩ�8+6��3.5��13��
��ӿ�ʼ�˶�������ǰ����t���P����M��N�ľ�����ȣ�
��������з���Ϊ��t������8+6t����6+2t��t��
���t��![]() ��
��
��ӿ�ʼ�˶���������t���P����M��N�ľ�����ȣ�
��������з���Ϊ����2t+6����t��t��[13��6��t��3.5��]��
���t��![]() ��
��
�𣺴ӿ�ʼ�˶�����![]() ���3.5���
���3.5���![]() ���P����M��N�ľ�����ȣ�
���P����M��N�ľ�����ȣ�

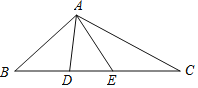
����Ŀ����ͼ����ABC������AB��AC�Ĵ�ֱƽ���߷ֱ�BC��D��E������BAC+��DAE=150�㣬���BAC�Ķ����ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
����Ŀ��ij�������е�һ����6000Ԫ�����ס���������Ʒ����������Ʒ�ļ����ȼ���Ʒ������![]() ����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע���������ۼ۩����ۣ�
����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע���������ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 22 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
��1���ó��й����ס���������Ʒ�����ټ���
��2���ó��н���һ�ι����ļס���������Ʒȫ�������һ���ɻ�ö�������
��3���ó��еڶ����Ե�һ�εĽ����ֹ����ס���������Ʒ�����м���Ʒ�ļ������䣬����Ʒ�ļ����ǵ�һ�ε�3��������Ʒ��ԭ�����ۣ�����Ʒ�������ۣ��ڶ���������Ʒ���������Ժ��õ�������ȵ�һ�λ�õ��������180Ԫ����ڶ�������Ʒ�ǰ�ԭ�۴������ۣ�
����Ŀ��Ŀǰȫ���ᳫ���������ܵ��ڳ����ѻ����ռ���ij�̳��ƻ������ס������ֽ��ܵƹ�1000ֻ�������ֽ��ܵƵĽ��ۣ��ۼ����±���
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���� | 25 | 30 |
���� | 45 | 60 |
��1����ν�����������ǡ��Ϊ37000Ԫ��
��2��Ϊȷ�����ͽ��ܵ�˳���������ڣ�1���������£��̼Ҿ��������ͽ��ܵƽ��д��۳��ۣ���ȫ����������ͽ��ܵƵ�������Ϊ20%���������ͽ��ܵ�����ۣ�