题目内容
【题目】如图,在一张直角三角形纸片ABC中,∠ACB=90°,∠A=30°P是边AB上的一动点,将△ACP沿着CP折叠至△A1CP,当△A1CP与△ABC的重叠部分为等腰三角形时,则∠ACP的度数为_____.

【答案】40°或70°
【解析】
分两种情形,画出图形分别求解即可.当PC=CE时,设∠ACP=x,利用等腰三角形的性质,可证得∠CPE=x+30°,再利用三角形内角和定理建立关于x的方程,解方程即可;当CP=CE时,设∠ACP=x,用含x的代数式表示出∠CPE、∠CEP,再利用三角形内角和定理建立关于x的方程,解方程即可求得结论.
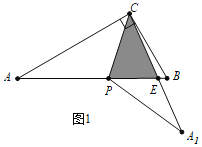
当PC=CE时,如图1所示:
设∠ACP=x,根据折叠的性质得∠A1CP=x,
∵CP=CE,
∴∠CPE=∠CEP,
∵∠CPE=∠ACP+∠A=x+30°,
∴在![]() 中:x+x+30°+x+30°=180°,
中:x+x+30°+x+30°=180°,
∴x=40°;

当CP=CE时,如图2所示:
设∠ACP=x.根据折叠的性质得∠A1CP=x,∠A1=∠A=30°,
则∠CPE=∠CEP=∠ECA+∠A1=∠ACP +∠A1CP -∠ACB= 2x﹣90°+30°=2x﹣60°,
在△CPE中,90°﹣x+2(2x﹣60°)=180°,
解得:x=70°,
综上所述,∠ACP的度数为40°或70°,
故答案为:40°或70°.

【题目】某年级共有300名学生,为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制)、并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
a.A课程成绩的频数分布直方图如下(数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100);
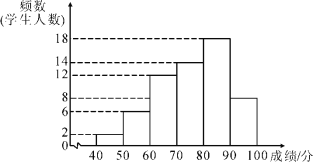
b.A课程成绩在70≤x<80这一组的是:
70 71 71 71 76 76 77 78 78.5 78.5 79 79 79 79.5
c.A,B两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
A | 75.8 | m | 84.5 |
B | 72.2 | 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中m的值;
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是______(填“A”或“B”),理由是________________________________;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过75.8分的人数.




