题目内容
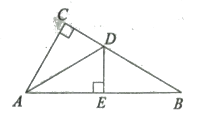
【题目】如图，在Rt△ABC中，∠C=90°，AD平分∠CAB,交CB于点D,DE⊥AB于点E.
(1)求证：△ACD≌△AED
(2)若AC=5，△DEB的周长为8，求△ABC的周长
【答案】（1）证明见解析；
（2）△ABC的周长是18．
【解析】试题分析：(1)、根据角平分线的性质得出DC=DE，结合AD=AD从而得出两个直角三角形全等；(2)、根据全等得出AE=AC=5，CD=ED，从而得出△ABC的周长=AC+AC+△DEB的周长得出答案.
试题解析：(1)、因为AD平分∠CAB，∠C=90°，DE⊥AB 所以DC=DE
在△ACD和△AED中，DC=DE，AD=AD 得△ACD≌△AED（HL）
（2）由（1）得△ACD≌△AED 所以AE=AC=5，CD=ED
=AC+AB+BC=AC+（AE+EB）+（BD+DC）=AC+AC+EB+BD+DE）=AC+AC+
=5+5+8=18．
练习册系列答案
相关题目
