题目内容
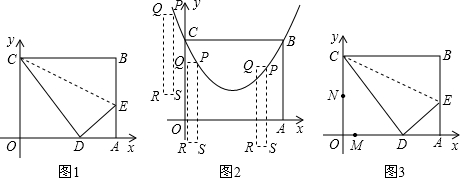
如图1,矩形OABC,O为原点,点E在AB上,把△CBE沿CE折叠,使点B落在OA边上的点D处,A、D坐标分别为(10,0)和(6,0),抛物线y=
x2+bx+c过点C、B.
(1)求B点的坐标及该抛物线的解析式;
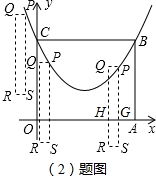
(2)如图2,矩形PQRS的长、宽一定,点P沿(1)中的抛物线滑动,在滑动过程中PQ∥x轴,且RS在PQ的下方,当P点横坐标为-1时,点S位于x轴上方且距离x轴
个单位.当矩形PQRS在滑动过程中被x轴分成上下两部分的面积比为2:3时,求点P的坐标;
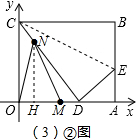
(3)如图3,动点M、N同时从点O出发,点M以每秒3个单位长度的速度沿线段OD运动,点N以每秒8个单位长度的速度沿折线OCD按O→C→D的路线运动,当M、N中的其中一点停止运动时,另一点也停止运动.设M、N同时从点O出发t秒时,△OMN的面积为S.求S与t的函数关系式,并写出t的取值范围.
| 1 |
| 5 |
(1)求B点的坐标及该抛物线的解析式;
(2)如图2,矩形PQRS的长、宽一定,点P沿(1)中的抛物线滑动,在滑动过程中PQ∥x轴,且RS在PQ的下方,当P点横坐标为-1时,点S位于x轴上方且距离x轴
| 11 |
| 5 |
(3)如图3,动点M、N同时从点O出发,点M以每秒3个单位长度的速度沿线段OD运动,点N以每秒8个单位长度的速度沿折线OCD按O→C→D的路线运动,当M、N中的其中一点停止运动时,另一点也停止运动.设M、N同时从点O出发t秒时,△OMN的面积为S.求S与t的函数关系式,并写出t的取值范围.

分析:(1)根据折叠的性质可知:CD=CB,因此在已知A、D的坐标情况下,能得到CB、CD、OD的长,在Rt△OCD中,利用勾股定理即可求出OC的长,则B点坐标可求;再利用待定系数法就能求得抛物线的解析式.
(2)将点P的横坐标-1代入(1)的抛物线解析式中即可求得点P到x轴的距离,再由“点S位于x轴上方且距离x轴
个单位”即可求出PS的长;当矩形PQRS的面积被x轴分割成上2下3时,由于两个小矩形的宽相同,所以它们的面积比等于长的比,即此时的PS被x轴分割成上2下3的情况,结合PS的长,即可得到此时点P的纵坐标,代入抛物线的解析式中就能求得点P的坐标.
(3)由于点N的运动过程为:O→C→D,所以整体要分两个阶段考虑:
①点N在线段OC上时,首先用t表达出OM、ON的长,以OM为底、ON为高,不难得到△OMN的面积S与t的函数关系式;
②点N在线段CN上时,OM的长易知,关键是求出OM上的高,先过点N作OD的垂线NH,由∠CDO的正弦值可求出NH的表达式,以OM为底、NH为高即可求得关于S、t的函数关系式.
(2)将点P的横坐标-1代入(1)的抛物线解析式中即可求得点P到x轴的距离,再由“点S位于x轴上方且距离x轴
| 11 |
| 5 |
(3)由于点N的运动过程为:O→C→D,所以整体要分两个阶段考虑:
①点N在线段OC上时,首先用t表达出OM、ON的长,以OM为底、ON为高,不难得到△OMN的面积S与t的函数关系式;
②点N在线段CN上时,OM的长易知,关键是求出OM上的高,先过点N作OD的垂线NH,由∠CDO的正弦值可求出NH的表达式,以OM为底、NH为高即可求得关于S、t的函数关系式.
解答:解:(1)由矩形OCBA得:∠COA=∠BAO=90°,OC=AB,BC=OA=10;
由△CBE沿CE翻折得到△CED,得 CD=CB=10,
由勾股定理得:OC=
=
=8,
得:C(0,8),B(10,8);
又C、B均在y=
x2+bx+c上,代入,得:
,解得
∴y=
x2-2x+8.
 (2)当x=-1时,y=
(2)当x=-1时,y=
×(-1)2-2×(-1)+8,此时P(-1,
);
又由S距离x轴上方
个单位,得:PS=
-
=8,∴矩形PQRS的长为8.
设PQRS在下滑过程中交x轴分别于G、H两点.
则由题意知:
=
,即
=
∴PG=
PS=
;
故P的纵坐标为
,设P(a,
),则:
a2-2a+8=
,得:a1=4,a2=6
∴P(4,
)或(6,
).
 (3)①当0≤t≤1时,此时M在OD上,N在OC上.
(3)①当0≤t≤1时,此时M在OD上,N在OC上.
∴S△MON=
OM•ON=
×3t×8t=12t2;
②当1<t≤2时,此时M在OD上,N在CD上.则DN=18-8t
过N作NH⊥OD于H,则
=
=
,得:
NH=
DN=
(18-8t)=
(9-4t)
∴S△ONM=
•NH•OM=
×
(9-4t)•3t=-
t2+
t;
综上,S=
.
由△CBE沿CE翻折得到△CED,得 CD=CB=10,
由勾股定理得:OC=
| CD2-OD2 |
| 102-62 |
得:C(0,8),B(10,8);
又C、B均在y=
| 1 |
| 5 |
|
|
∴y=
| 1 |
| 5 |
 (2)当x=-1时,y=
(2)当x=-1时,y=| 1 |
| 5 |
| 51 |
| 5 |
又由S距离x轴上方
| 11 |
| 5 |
| 51 |
| 5 |
| 11 |
| 5 |
设PQRS在下滑过程中交x轴分别于G、H两点.
则由题意知:
| S矩形PQHG |
| S矩形HGSR |
| 2 |
| 3 |
| PG |
| GS |
| 2 |
| 3 |
∴PG=
| 2 |
| 5 |
| 16 |
| 5 |
故P的纵坐标为
| 16 |
| 5 |
| 16 |
| 5 |
| 1 |
| 5 |
| 16 |
| 5 |
∴P(4,
| 16 |
| 5 |
| 16 |
| 5 |
 (3)①当0≤t≤1时,此时M在OD上,N在OC上.
(3)①当0≤t≤1时,此时M在OD上,N在OC上.∴S△MON=
| 1 |
| 2 |
| 1 |
| 2 |
②当1<t≤2时,此时M在OD上,N在CD上.则DN=18-8t
过N作NH⊥OD于H,则
| NH |
| ND |
| OC |
| CD |
| 4 |
| 5 |
NH=
| 4 |
| 5 |
| 4 |
| 5 |
| 8 |
| 5 |
∴S△ONM=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 5 |
| 48 |
| 5 |
| 108 |
| 5 |
综上,S=
|
点评:题目的叙述和给出的图形看起来较为复杂,但通过读题后可以发现题目的难度并不大;(1)题中,利用好折叠图形的特点是关键;(2)题中,只要求出PS的长题目也就解了一大半;最后一题求的是分段函数,三角形面积的求法应熟练掌握,在对自变量进行分段时,要注意抓住“关键点”(即点N、C重合时),这在解答此类题目时是通用的方法.

练习册系列答案
相关题目

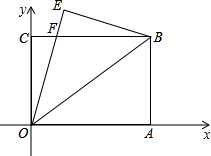 如图,将矩形OABC在直角坐标系中A(4,0),B(4,3),将矩形OABC沿OB对折,使点A落在E处,并交BC于点F,则BF=
如图,将矩形OABC在直角坐标系中A(4,0),B(4,3),将矩形OABC沿OB对折,使点A落在E处,并交BC于点F,则BF= 如图,在矩形OABC中,OA=8,OC=4,OA,OC分别在x,y轴上,点D在OA上,且CD=AD.
如图,在矩形OABC中,OA=8,OC=4,OA,OC分别在x,y轴上,点D在OA上,且CD=AD.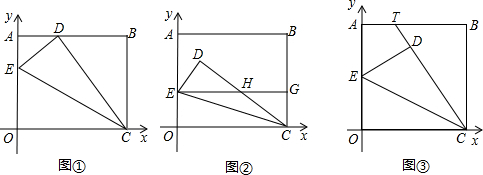
 上的一个动点(不与点O重合).
上的一个动点(不与点O重合).