题目内容
如图,在直角坐标系中,第一次将△OAB变换成△OA1 B1,第二次将△OA1 B1变换成OA2B2,第三次将△OA2B2变换成△OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3(8,3);B(2,O),B1(4,0),B2(8,0),B3(16,0).
①观察每次变换前后的三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成△OA4 B4,则A4的坐标是________,B4的坐标是________;②若按第①题找到的规律将△OAB进行了N次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,找出规律,推测An的坐标是________,Bn的坐标是________.
答案:
解析:
解析:
| ①(16,3) (32,0) ②(2n,3)(2n+1,0)
|

练习册系列答案
相关题目
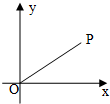 如图,在直角坐标平面内,点P与原点O的距离OP=2,线段OP与x轴正半轴的夹角为30°,则点P的坐标是( )
如图,在直角坐标平面内,点P与原点O的距离OP=2,线段OP与x轴正半轴的夹角为30°,则点P的坐标是( )| A、(2,1) | ||
| B、(1,2) | ||
C、(
| ||
D、(1,
|
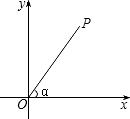 如图,在直角坐标平面内有一点P(3,4),那么OP与x轴正半轴的夹角a的正弦值为( )
如图,在直角坐标平面内有一点P(3,4),那么OP与x轴正半轴的夹角a的正弦值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
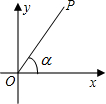 如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与x轴正半轴的夹角为α,且
如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与x轴正半轴的夹角为α,且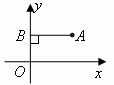
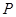 与原点
与原点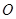 的距离
的距离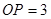 ,线段
,线段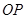 与
与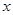 轴正半轴的夹角为
轴正半轴的夹角为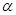 ,且
,且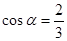 ,则点
,则点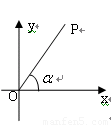
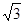 );
); 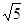 ,2);
(D)(2,
,2);
(D)(2,