题目内容
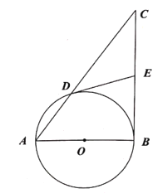
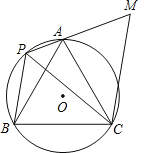
【题目】如图,等边△ABC内接于⊙O,P是![]() 上任意一点(不与点A、B重合),连AP、BP,过点C作CM//BP交PA的延长线于点M.
上任意一点(不与点A、B重合),连AP、BP,过点C作CM//BP交PA的延长线于点M.
(1)求∠APC和∠BPC的度数
(2)探究PA、PB、PM之间的关系
(3)若PA=1,PB=2,求四边形PBCM的面积.
【答案】(1)∠APC=60°;∠BPC=60°;(2)PM= PA+PB;(3)![]()
【解析】
(1)根据等边三角形的性质和同弧所对的圆周角相等即可得出结论;
(2)根据平行线的性质可得∠MCP=∠BPC=60°,然后根据等边三角形的判定可得△CPM为等边三角形,再利用SAS证出△BCP≌△ACM,即可得出PB=AM,从而得出结论;
(3)过点C作CD⊥MP于D,根据(2)的结论和等边三角形的性质求出AM和CD,利用三角形的面积公式即可求出S△CAM和S△CAP,然后根据全等三角形的性质可得S△BCP= S△ACM,最后根据S四边形PBCM = S△CAM+S△CAP+S△BCP即可得出结论.
解:(1)∵△ABC为等边三角形
∴∠BAC=∠ABC=∠ACB=60°,AB=AC=BC
∴∠APC=∠ABC=60°,∠BPC=∠BAC=60°;
(2)PM= PA+PB,理由如下
∵CM∥BP
∴∠MCP=∠BPC=60°
∴∠M=180°-∠MPC-∠MCP=60°
∴△CPM为等边三角形
∴CP=CM,∠PCM=60°
∵∠ACB=60°
∴∠ACB=∠PCM
∴∠BCP=∠ACM
在△BCP和△ACM中
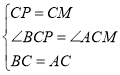
∴△BCP≌△ACM
∴PB=AM
∴PM=PA+AM=PA+PB
(3)过点C作CD⊥MP于D
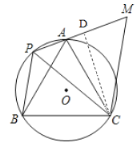
∵PA=1,PB=2,
∴PM=PA+PB=3,AM=PB=2
∵△CPM为等边三角形
∴CM=CP=PM=3,
∵CD⊥MP
∴MD=![]() =
=![]()
根据勾股定理可得CD=![]()
∴S△CAM=![]()
S△CAP=![]()
∵△BCP≌△ACM
∴S△BCP= S△ACM![]()
∴S四边形PBCM = S△CAM+S△CAP+S△BCP![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案