题目内容
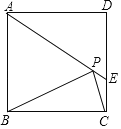
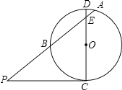
【题目】已知:如图,![]() 为
为![]() 的弦,
的弦,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 切
切![]() 于
于![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 交
交![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A. 9 B. 12 C. 15 D. 6
【答案】C
【解析】
过O作OF垂直于AB,利用垂径定理得到F为AB的中点,由AB的长求出AF的长,再由AF-AE求出EF的长,利用相交弦定理得到AEBE=DEEC,求出EC的长,由DE+EC求出直径DC的长,确定出半径OD的长,由OD-DE求出OE的长,由CP为圆O的切线,得到EC垂直于CP,得到一对直角相等,再由一对公共角,利用两对对应角相等的两三角形相似得到三角形EFO与三角形ECP相似,由相似得比例,将各自的值代入即可求出PB的长.
过O作OF⊥AB,交AB于点F,
又AE=3,BE=6,
∴AF=BF=![]() AB=
AB=![]() (AE+BE)=4.5,
(AE+BE)=4.5,
∴EF=AF-AE=4.5-3=1.5,
由相交弦定理得到AEBE=DEEC,
∵DE=2,AE=3,BE=6,
∴EC=![]() =9,
=9,
∴圆的直径DC=DE+EC=2+9=11,半径OD=5.5,
∴OE=OD-DE=5.5-2=3.5,
∵CP为圆O的切线,∴∠ECP=90°,
∴∠EFO=∠ECP=90°,且∠FEO=∠CEP,
∴△EFO∽△ECP,
∴![]() ,即
,即![]() ,
,
解得:PB=15.
故选:C.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目