Question

【题目】如图，已知楼高米，从楼顶处测得对面小平房的俯角为，又乘电梯到离地米的一窗户处测得小平房顶的仰角为，则小平房到大楼的距离为________米．（结果保留根号形式）

Answer 1

【答案】

【解析】

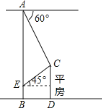
如图：首先过点C作CF⊥AB于F，易证四边形EFCG与四边形BEGD是矩形，设CG=xm，在Rt△CEG和Rt△AFC中，根据角的度数表示出AF，EF的长，又由楼AB的高为25米，列出方程，求出x的值，即可得出答案．

过点C作CF⊥AB于F，

∴CF∥EG∥AM，

∴∠MAC=∠ACF=60，

∴四边形EFCG与四边形BEGD是矩形，

∴EF=CG，DG=BE=5，FC=EG，

设CG=xm，

∴EF=CG=xm，

在Rt△CEG中,∠CGE=90,∠CEG=45，

∴CG=EG=CF=EF=x(m)，

在Rt△AFC中,AF=FCtan60=x(m)，

∵AB=25m，

∴x+x+5=25，

解得：x=10(1)=1010，

∴AF=x=×(1010)=3010 (m).

答：小平房到大楼的距离为(3010)m.

故答案为：(3010)m.