题目内容
如图，⊙O为△ABC的外接圆，已知∠A=34°，∠ABC=82°，则∠ABO=________°．
26
分析：连接OA，在△ABC中利用内角和定理求得∠ACB的度数，然后根据圆周角定理求得∠AOB的度数，然后在等腰△AOB中利用等边对等角即可求解．
解答：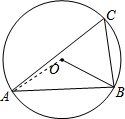
解：连接OA．
∵∠ACB=180°-∠A-∠ABC=180°-34°-82°=64°，
∴∠AOB=2∠ACB=128°，
∵OA=OB，
∴∠ABO=∠BAO=
=
=26°．
故答案是：26．
点评：本题考查了圆周角定理以及等腰三角形的性质定理，正确作出辅助线是关键．
分析：连接OA，在△ABC中利用内角和定理求得∠ACB的度数，然后根据圆周角定理求得∠AOB的度数，然后在等腰△AOB中利用等边对等角即可求解．
解答：
解：连接OA．∵∠ACB=180°-∠A-∠ABC=180°-34°-82°=64°，
∴∠AOB=2∠ACB=128°，
∵OA=OB，
∴∠ABO=∠BAO=
==26°．故答案是：26．
点评：本题考查了圆周角定理以及等腰三角形的性质定理，正确作出辅助线是关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
24、如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G．
14、如图，E为△ABC的重心，ED=3，则AD=
（2012•井研县模拟）如图，D为△ABC的AB边上的一点，∠ABC=∠ACD，AD=2cm，AB=3cm，则AC=（ ）
如图，D为△ABC的边AB上一点，且∠ABC=∠ACD，AD=3cm，AB=4cm，则AC的长为（ ）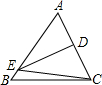
如图，DE为△ABC中AC边的中垂线，BC=8，AB=10，则△EBC的周长是（ ）