Question

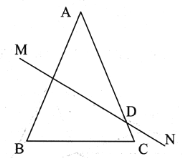
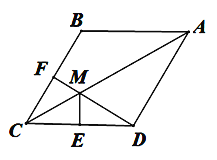
【题目】（本题满分10分）如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E, ∠BAC=∠CDF.

(1）求证BC=2CE；

(2）求证AM=DF+ME.

Answer 1

【答案】(1)BC= 2CE(2)AM=DF+ME

【解析】

试题（1）由条件可证得CE=DE，结合菱形的性质可证得BC=2CE；

（2）分别延长AB、DF交于点G，可证△CDF≌△BGF，则可证得GF=DF，结合条件可证得AM=GM，MF=ME，则可证得结论．

试题解析：(1)∵四边形ABCD为菱形，

∴AB∥CD，且BC=CD，

∴∠BAC=∠ACD，且∠BAC=∠CDF，

∴∠ACD=∠CDF，

∴CM=DM，

∵ME⊥CD，

∴CE=DE，

∴BC=CD=2CE；

（2）如图，分别延长AB，DF交于点G，

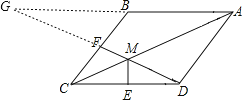
∵AB∥CD，

∴∠G=∠CDF=∠BAC，

∴MG=MA，

在△CDF和△BGF中，，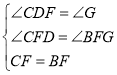

∴△CDF≌△BGF(AAS)，

∴GF=DF，

在△CEM和△CFM中，，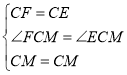

∴△CEM≌△CFM(SAS)，

∴ME=MF，

∴AM=GM=GF+MF=DF+ME.