Question

【题目】正方形ABCD和正方形AEFG有公共顶点A，将正方形AEFG绕点A按顺时针方向旋转，记旋转角∠DAG=α，其中0°≤α≤180°，连结DF，BF，如图．

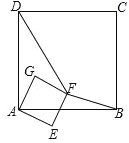
（1）若α=0°，则DF=BF，请加以证明；

（2）试画一个图形（即反例），说明（1）中命题的逆命题是假命题；

（3）对于（1）中命题的逆命题，如果能补充一个条件后能使该逆命题为真命题，请直接写出你认为需要补充的一个条件，不必说明理由．

Answer 1

【答案】（1）证明见解析；（2）作图见解析；（3）若点F在正方形ABCD内．

【解析】

试题分析：（1）利用正方形的性质证明△DGF≌△BEF即可；

（2）当α=180°时，DF=BF．

（3）利用正方形的性质和△DGF≌△BEF的性质即可证得是真命题．

试题解析：（1）如图1，∵四边形ABCD和四边形AEFG为正方形，

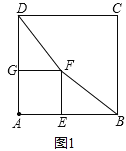
∴AG=AE，AD=AB，GF=EF，∠DGF=∠BEF=90°，

∴DG=BE，

在△DGF和△BEF中，

，

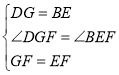∴△DGF≌△BEF（SAS），

∴DF=BF；

（2）图形（即反例）如图2，

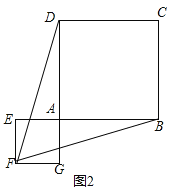
（3）补充一个条件为：点F在正方形ABCD内；

即：若点F在正方形ABCD内，DF=BF，则旋转角α=0°．