��Ŀ����
����Ŀ������ͬѧ����һ����ϣ����������������г���M�س�����һ����·����ǰ��N�أ�������ʻ��ʱ��Ϊt��h������������֮��ľ���Ϊy��km����y��t�ĺ�����ϵ��ͼ1��ʾ��
����˼����������ͼ1�IJ�����ȷ��Ϣ�����ȳ���1h���׳���0.5Сʱ����������
�����������ͬѧ����������⣺
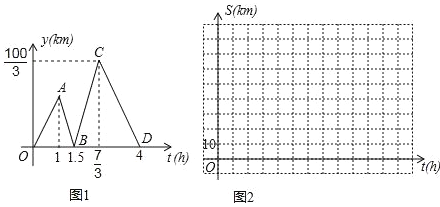
��1���ֱ�����߶�BC��CD����ֱ�ߵĺ�������ʽ��
��2����20��y��30ʱ����t��ȡֵ��Χ��
��3���ֱ�����ף�����ʻ��·��S����S����ʱ��t�ĺ�������ʽ������ͼ2������ֱ������ϵ�зֱ����ǵ�ͼ��
��4������Ħ�г�����ͬʱ��������N����ͬһ��·����ǰ��M�أ���������![]() h�����������ʱ����������ʱ�����������
h�����������ʱ����������ʱ�����������
���𰸡�������y=40t-60��y=-20t+80����2��2��t��![]() ��
��![]() ��t��3����3��S��=60t-60��1��t��
��t��3����3��S��=60t-60��1��t��![]() ����S��=20t��0��t��4������4��������
����S��=20t��0��t��4������4��������![]() h���������
h���������
��������
�����������1�����ô���ϵ������������ʽ�����ɽ��
��2��������ס��ҵ��ٶȡ�����OA�ĺ�������ʽΪ��y=20t��0��t��1�������Ե�A��������Ϊ20�����ݵ�20��y��30ʱ���õ�20��40t-60��30����20��-20t+80��30���ⲻ��ʽ�鼴�ɣ�
��3���õ�S��=60t-60��1��t��![]() ����S��=20t��0��t��4������������ͼ�ɣ�
����S��=20t��0��t��4������������ͼ�ɣ�
��4��ȷ������M�ص�·��S����ʱ��t�ĺ�������ʽΪ��S��=-40t+80��0��t��2��������S��=-40t+80��S��=60t-60��ͼ��ĺ�����Ϊ![]() �����Ա�����
�����Ա�����![]() h���������
h���������
�����������1��ֱ��BC�ĺ�������ʽΪy=kt+b��
�ѣ�1.5��0������![]() ��
��![]() ������ã�
������ã�
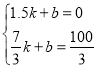
��ã�![]() ��
��
��ֱ��BC�Ľ���ʽΪ��y=40t-60��
��ֱ��CD�ĺ�������ʽΪy1=k1t+b1��
�ѣ�![]() ��
��![]() ������4��0������ã�
������4��0������ã�
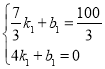 ��
��
��ã�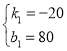 ��
��
��ֱ��CD�ĺ�������ʽΪ��y=-20t+80��
��2������ٶ�Ϊakm/h���ҵ��ٶ�Ϊbkm/h����������ã�
 ��
��
��ã�![]() ��
��
�����ٶ�Ϊ60km/h���ҵ��ٶ�Ϊ20km/h��
��OA�ĺ�������ʽΪ��y=20t��0��t��1�������Ե�A��������Ϊ20��
��20��y��30ʱ��
��20��40t-60��30����20��-20t+80��30��
��ã�2��t��![]() ��
��![]() ��t��3��
��t��3��
��3����������ã�S��=60t-60��1��t��![]() ����S��=20t��0��t��4����
����S��=20t��0��t��4����
����ͼ����ͼ2��ʾ��
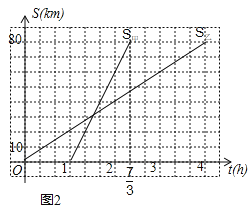
��4����t=![]() ʱ��S��=
ʱ��S��=![]() ������M�ص�·��S����ʱ��t�ĺ�������ʽΪ��
������M�ص�·��S����ʱ��t�ĺ�������ʽΪ��
S��=-40t+80��0��t��2����
��ͼ3��
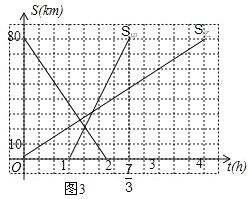
S��=-40t+80��S��=60t-60��ͼ��ĺ�����Ϊ![]() �����Ա�����
�����Ա�����![]() h���������
h���������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�