题目内容
【题目】我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,
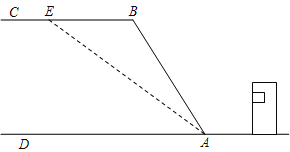
(1)求山坡高度;
(2)为防夏季因暴雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC削进到E处,问BE至少是多少米(结果保留根号)?
【答案】(1)山坡的高度为20![]() 米;(2)BE至少20(
米;(2)BE至少20(![]() -1)米.
-1)米.
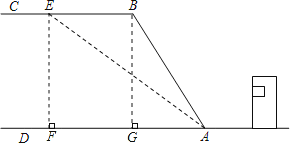
【解析】试题分析:(1)作BG⊥AD于G.构建直角△ABG,通过解该直角三角形求得BG的长度,即山坡高度;
(2)作EF⊥AD于F.通过解直角△ABG得到线段AG的长度,然后解直角△AEF求得AF=EF=BG=20![]() .所以BE=FG=AF-AG.
.所以BE=FG=AF-AG.
试题解析:(1)作BG⊥AD于G.
∵Rt△ABG中,∠BAD=60°,AB=40,
∴BG=AB![]() sin60°=20
sin60°=20![]() ,
,
∴山坡的高度为20![]() 米;
米;
(2)作EF⊥AD于F.
AG=AB![]() cos60°=20.
cos60°=20.
同理在Rt△AEF中,∠EAD=45°,
∴AF=EF=BG=20![]() ,
,
∴BE=FG=AF-AG=20(![]() -1)米
-1)米
∴BE至少20(![]() -1)米.
-1)米.

练习册系列答案
相关题目