题目内容
【题目】如图,在平面直角坐标系中,矩形OACB的顶点O是坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点.若E为边OA上的一个动点,当△CDE的周长最小时,则点E的坐标____________.
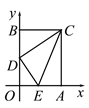
【答案】(1,0)
【解析】分析:由于C、D是定点,则CD是定值,如果![]() 的周长最小,即
的周长最小,即![]() 有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时
有最小值.为此,作点D关于x轴的对称点D′,当点E在线段CD′上时![]() 的周长最小.
的周长最小.
详解:
如图,作点D关于x轴的对称点D′,连接CD′与x轴交于点E,连接DE.
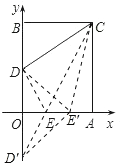
若在边OA上任取点E′与点E不重合,连接CE′、DE′、D′E′
由DE′+CE′=D′E′+CE′>CD′=D′E+CE=DE+CE,
可知△CDE的周长最小,
∵在矩形OACB中,OA=3,OB=4,D为OB的中点,
∴BC=3,D′O=DO=2,D′B=6,
∵OE∥BC,
∴Rt△D′OE∽Rt△D′BC,有![]()
∴OE=1,
∴点E的坐标为(1,0).
故答案为:(1,0).

练习册系列答案
相关题目