题目内容
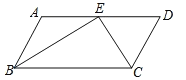
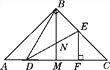
【题目】如图，在△ABC中，AB＝BC，∠ABC＝90°，BM是AC边上的中线，点D，E分别在边AC和BC上，DB＝DE，DE与BM相交于点N，EF⊥AC于点F，以下结论：
①∠DBM＝∠CDE；②S△BDE<S四边形BMFE；③CD·EN＝BN·BD；④AC＝2DF.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题分析：由AB=BC，∠ABC=90°，BM是AC边中线可知△ABC、△ABM、△CBM都是等腰直角三角形，因为DB=DE，所以对应两个底角相等．（1）∵∠DEB=∠EDC+∠C=∠EDC+45°（三角形外角性质），∴∠EDC=∠DEB-45°，因为∠DBE=∠DBM+∠MBE=∠DBM+45°，所以∠DBM=∠DBE-45°，而∠DBE=∠DEB，∴∠DBM=∠CDE，故（1）正确．（2）先证明△BDM≌△DEF，∵∠DBM=∠EDF（已证），∠DMB=∠EFD=90°，DB=DE，∴Rt△BDM≌Rt△DEF．∴S△BDM=S△DEF．∴S△BDM﹣S△DMN=S△DEF﹣S△DMN，即S△DBN=S四边形MNEF．∴S△DBN+S△BNE=S四边形MNEF+S△BNE，即S△BDE=S四边形BMFE，故（2）错误；（3）由所给CDEN=BNBD，化成比例式：CD:BD=BN:EN,所以只要能证明△DBC∽△NEB即可．∵∠BNE=∠DBM+∠BDN（三角形外角性质），∠BDM=∠BDE+∠EDF，∠EDF=∠DBM，∴∠BNE=∠BDM．即∠BNE=∠BDC，又∵∠C=∠NBE=45°，∴△DBC∽△NEB．∴对应线段成比例CD:BD=BN:EN，化成乘积式即得CDEN=BNBD，故（3）正确；（4）把所给线段进行转换：∵Rt△BDM≌Rt△DEF，∴BM=DF，∵BM是等腰直角三角形ABC斜边AC中线，∴BM=
AC，∴DF=AC，∴AC=2DF．故（4）正确．综上所述，选项中有三个正确，故选C．
