题目内容
直线y=- x+
x+ 与x轴,y轴交于A、B两点,若把△ABO沿直线AB翻折,点O落在第一象限的C处,则C点的坐标为
与x轴,y轴交于A、B两点,若把△ABO沿直线AB翻折,点O落在第一象限的C处,则C点的坐标为
- A.(
 ,
, )
) - B.(
 ,
, )
) - C.(
 ,
, )
) - D.(
 ,
, )
)
B
分析:本题应先根据题意得出A、B两点的坐标,再根据勾股定理即可解出C点的坐标.
解答:过C作CD⊥x轴,
∵y=- x+
x+ 与x轴,y轴交于A、B两点分别是(1,0),(0,
与x轴,y轴交于A、B两点分别是(1,0),(0, ),
),
∴AB=2,则∠ABO=30°,CD= ,AD=
,AD= ,OD=
,OD= ,则C点的坐标为(
,则C点的坐标为( ,
, ).
).
故选B.
点评:主要考查了点的坐标的意义以及与图形相结合的具体运用.要把点的坐标有机的和图形结合起来求解.
分析:本题应先根据题意得出A、B两点的坐标,再根据勾股定理即可解出C点的坐标.
解答:过C作CD⊥x轴,
∵y=-
 x+
x+ 与x轴,y轴交于A、B两点分别是(1,0),(0,
与x轴,y轴交于A、B两点分别是(1,0),(0, ),
),∴AB=2,则∠ABO=30°,CD=
 ,AD=
,AD= ,OD=
,OD= ,则C点的坐标为(
,则C点的坐标为( ,
, ).
).故选B.
点评:主要考查了点的坐标的意义以及与图形相结合的具体运用.要把点的坐标有机的和图形结合起来求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
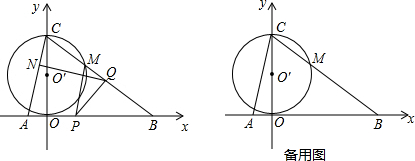
 (2012•兰州)如图,M为双曲线y=
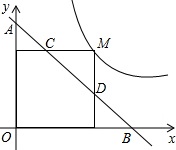
(2012•兰州)如图,M为双曲线y= (2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=
(2013•宛城区一模)如图,直线y=-2x+2与x轴y轴分别相交于点A、B,四边形ABCD是正方形,曲线y=