Question

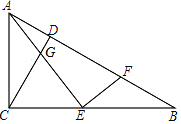
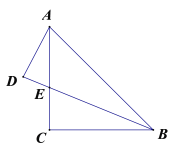
【题目】如图，等腰直角△ABC中，AC=BC，BE平分∠ABC，AD⊥BE的延长线于点D，若AD=2，则△ABE的面积为（ ）．

A.4B.6C.2D.2

Answer 1

【答案】A

【解析】

过点E作于F，设，运用等腰直角三角形将其它各未知线段用表示；延长AD与BC的延长线交于点G，依据ASA判定△ABD≌△GBD，依据全等的性质求得DG=AD=2，，继而得到AG=4，；接着在直角△ACG中，运用勾股定理列出关于的方程，解出代入到中即可.

解：延长AD与BC的延长线交于点G，过点E作于F，

易得是等腰直角三角形，

∴

∵BE平分∠ABC，EC⊥BC，,

∴EF=EC,,

∴

设

则，，

∵AD⊥BE,

∴,

∵在△ABD和△GBD中，

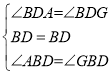
∴△ABD≌△GBD（ASA）

∴DG=AD=2,

∴AG=4,

∵在直角△ACG中，ACG=90°，，AG=4，，

∴

∴

∴=4.

故选：A.