题目内容
如图,抛物线 与
与 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当 =O和
=O和 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。

(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥ 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
(1)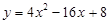 (2)S=2t2+4t,
(2)S=2t2+4t,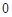 <
<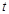 ≤
≤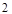 (3)点
(3)点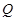 在线段
在线段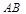 的中点上,16,平行四边形(4)
的中点上,16,平行四边形(4)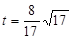
【解析】解:(1)∵当 和
和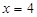 时,
时,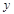 的值相等,∴
的值相等,∴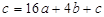 ,……1分
,……1分
∴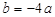 ,∴
,∴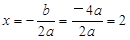
将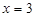 代入
代入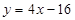 ,得
,得 ,
,
将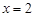 代入
代入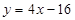 ,得
,得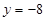 ………………………………………….2分
………………………………………….2分
∴设抛物线的解析式为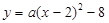
将点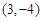 代入,得
代入,得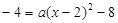 ,解得
,解得 .
.
∴抛物线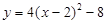 ,即
,即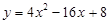 ……………………………..3分
……………………………..3分
(2)设直线OM的解析式为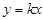 ,将点M
,将点M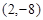 代入,得
代入,得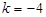 ,
,
∴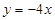 ……………………………………………………………………..4分
……………………………………………………………………..4分
则点P ,
, ,而
,而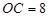 ,
,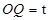 .
.
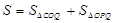 =
=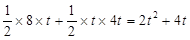 .......................5分
.......................5分
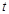 的取值范围为:
的取值范围为: <
<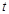 ≤
≤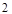 .......................................6分
.......................................6分
(1)随着点 的运动,四边形
的运动,四边形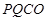 的面积
的面积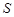 有最大值.
有最大值.
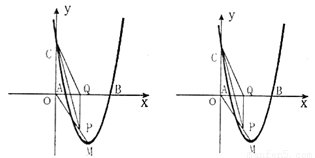
从图像可看出,随着点 由
由 →
→ 运动,
运动, 的面积与
的面积与 的面积在不断增大,即
的面积在不断增大,即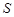 不断变大,显当然点
不断变大,显当然点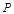 运动到点
运动到点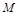 时,
时,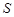 有最值...............7分
有最值...............7分
此时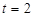 时,点
时,点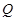 在线段
在线段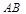 的中点上............. ................8分
的中点上............. ................8分
因而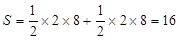 .
.
当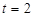 时,
时,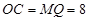 ,
,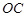 ∥
∥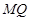 ,∴四边形
,∴四边形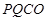 是平行四边形. ..9分
是平行四边形. ..9分
(4)随着点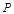 的运动,存在
的运动,存在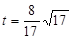 ,能满足
,能满足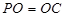 .................10分
.................10分
设点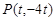 ,
,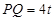 ,
,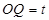 . 由勾股定理,得
. 由勾股定理,得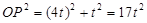 .
.
∵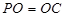 ,∴
,∴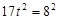 ,
,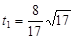 <
<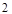 ,
,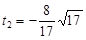 (不合题意)
(不合题意)
∴当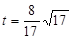 时,
时,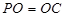 ...................................11分
...................................11分
(1)x=O和x=4时,y的值相等,即可得到函数的对称轴是x=2,把x=2和x=3分别代入直线y=4x-16就可以求出抛物线上的两个点的坐标,并且其中一点是顶点,利用待定系数法,设出函数的顶点式一般形式,就可以求出函数的解析式;
(2)根据待定系数法可以求出直线OM的解析式,设OQ的长为t,即P,Q的横坐标是t,把x=t代入直线OM的解析式,就可以求出P点的纵坐标,得到PQ的长,四边形PQCO的面积S=S△COQ+S△OPQ,很据三角形的面积公式就可以得到函数解析式;
(3)从图象可看出,随着点P由O→M运动,△COQ的面积与△OPQ的面积在不断增大,即S不断变大,显当然点P运动到点M时,S最值;
(4)在直角△OPQ中,根据勾股定理就可以求出点P的坐标.

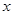 轴交于
轴交于 (2)点
(2)点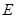 为抛物线上一动点,在
为抛物线上一动点,在 ,使以
,使以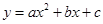 与
与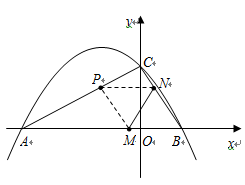
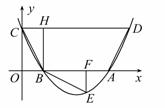
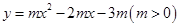 与
与 轴交于
轴交于 两点,与
两点,与 轴交于
轴交于 点.
点.
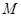 的坐标(用含
的坐标(用含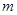 的代数式表示),
的代数式表示), 与
与 的面积比不变,试求出这个比值;
的面积比不变,试求出这个比值;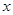 轴交于
轴交于 (
( ,0)、
,0)、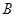 (
( ,0)两点,且
,0)两点,且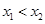 ,与
,与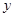 轴交于点
轴交于点 ,其中
,其中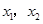 是方程
是方程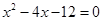 的两个根。(14分)
的两个根。(14分) (2)点
(2)点 是线段
是线段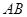 上的一个动点,过点
上的一个动点,过点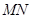 ∥
∥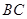 ,交
,交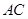 于点
于点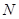 ,连接
,连接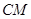 ,当
,当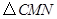 的面积最大时,求点
的面积最大时,求点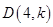 在(1)中抛物线上,
在(1)中抛物线上,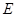 为抛物线上一动点,在
为抛物线上一动点,在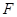 ,使以
,使以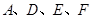 为顶
为顶