��Ŀ����
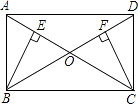
����Ŀ����֪�ھ���ABCD�У���ADC��ƽ����DE��BC�����ڵ�ֱ�߽��ڵ�E����P���߶�DE��һ���㣨����EP��PD��
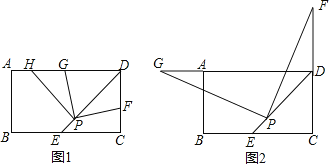
��1����ͼ1������F��CD���ϣ�����D�غϣ�������DPF�Ƶ�P��ʱ����ת90���ǵ�����PD��PF�ֱ�����DA�ڵ�H��G��
����֤��PG=PF��
��̽����DF��DG��DP֮����������������ϵ����֤����Ľ��ۣ�
��2����չ����ͼ2������F��CD���ӳ����ϣ�����D�غϣ�������P��PG��PF��������DA�ڵ�G������Ϊ��1����DE��DG��DP֮���������ϵ�Ƿ���Ȼ������������������֤����������������д�������������������ϵʽ����˵�����ɣ�
���𰸡���1����֤������������DG+DF=![]() DP����2����������������ϵʽӦΪ��DG��DF=
DP����2����������������ϵʽӦΪ��DG��DF=![]() DP��
DP��
�������������������1������֤PG=PF����֤��HPG�ա�DPF����֪��DPH=��HPG������ת��֪��GPF=��HPD=90�㼰DEƽ�֡�ADC�á�HPDΪ����ֱ�������Σ�����DHP=��PDF=45�㡢PD=PH�����ɵ�֤��
���ɡ�HPDΪ����ֱ�������Σ���HPG�ա�DPF֪HD=![]() DP��HG=DF������DG+DF=DG+GH=DH���ɵã�
DP��HG=DF������DG+DF=DG+GH=DH���ɵã�
�����������2������P��PH��PD������DA�ڵ�H����֤��HPDΪ����ֱ�������οɵ�PH=PD��HD=![]() DP����֤��HPG�ա�DPF�ɵ�HG=DF������DH=DG-HG=DG-DF�ɵ�DG-DF=
DP����֤��HPG�ա�DPF�ɵ�HG=DF������DH=DG-HG=DG-DF�ɵ�DG-DF=![]() DP��
DP��
��1���١ߡ�GPF=��HPD=90�㣬��ADC=90�㣬
���GPH=��FPD��
��DEƽ�֡�ADC��
���PDF=��ADP=45�㣬
���HPDΪ����ֱ�������Σ�
���DHP=��PDF=45�㣬
�ڡ�HPG�͡�DPF�У�
��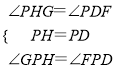 ��
��
���HPG�ա�DPF��ASA����
��PG=PF��
�ڽ��ۣ�DG+DF=![]() DP��
DP��
�ɢ�֪����HPDΪ����ֱ�������Σ���HPG�ա�DPF��
��HD=![]() DP��HG=DF��
DP��HG=DF��
��HD=HG+DG=DF+DG��
��DG+DF=![]() DP��
DP��
��2����������������ϵʽӦΪ��DG-DF=![]() DP��
DP��
��ͼ������P��PH��PD������DA�ڵ�H��
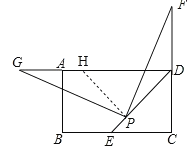
��PF��PG��
���GPF=��HPD=90�㣬
���GPH=��FPD��
��DEƽ�֡�ADC�����ھ���ABCD�У���ADC=90�㣬
���HDP=��EDC=45�㣬�õ���HPDΪ����ֱ�������Σ�
���DHP=��EDC=45�㣬��PH=PD��HD=![]() DP��
DP��
���GHP=��FDP=180��-45��=135�㣬
�ڡ�HPG�͡�DPF�У�
��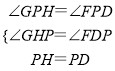
���HPG�ա�DPF��
��HG=DF��
��DH=DG-HG=DG-DF��
��DG-DF=![]() DP��
DP��

 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�