题目内容
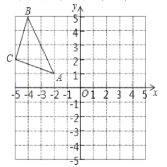
【题目】如图,在菱形ABCD中,对角线AC,相交于点O,![]() cm,
cm,![]() cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设
cm,E,F分别是AB,BC的中点,点P是对角线AC上的一个动点,设![]() cm,
cm,![]() cm,
cm,![]() cm
cm
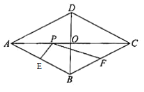
小明根据学习函数的经验,分别对这两种函数随自变量的变化而变化的情况进行了探究,下面是小明探究过程,请补充完整:
(1)画函数![]() 的图象
的图象
①按下表自变量的值进行取点、画图、测量,得到了![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 1.12 | 0.5 | 0.71 | 1.12 | 1.58 | 2.06 | 2.55 | 3.04 |
②在所给坐标系中描出补全后的表中的各对应值为坐标的点,画出函数![]() 的图象;
的图象;

(2)画函数![]() 的图象
的图象
在同一坐标系中,画出函数![]() 的图象;
的图象;
(3)根据画出的函数![]() 的图象、函数
的图象、函数![]() 的图象,解决问题
的图象,解决问题
①函数![]() 的最小值是________________;
的最小值是________________;
②函数![]() 的图象与函数
的图象与函数![]() 的图象的交点表示的含义是________________;
的图象的交点表示的含义是________________;
③若![]() ,AP的长约为________________cm
,AP的长约为________________cm
【答案】(1)①见解析;②见解析;(2)见解析;(3)①y1的最小值是0.5;②AP的长为2cm;③x=2.50.
【解析】
(1)①由表格得点(x,y1)即可;
②先由①描点,再用光滑曲线顺次连接各点,即可得出函数图象;利用数形结合,根据当x=0.5时,得出y1值,填入表格即可;
(2)过点F作FM⊥AC于M,由菱形的性质各三角形中位线性质求得FM=1,PM=3-x,所以y2=![]() ,再利用描点法画出y2的图象即可;
,再利用描点法画出y2的图象即可;
(3)①利用数形结合,由函数y1的图象求解即可;
②过点F作FM⊥AC于M,
可利用几何背景意义求解;
③因PC=AC-AP=4-x,由PE=PC,则y1=4-x,利用图象求解即可.
解:(1)①如下表:图象如图所示:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
y1/cm | 1.12 | 0.71 | 0.5 | 0.71 | 1.12 | 1.58 | 2.06 | 2.55 | 3.04 |
②过点F作FM⊥AC于M,如图,
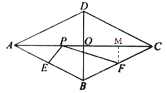
∵菱形ABCD,
∴AC⊥BD,
∴FM∥BD,
∵F是BC的中点,
∴M是OC的中点,
∴FM=1,OM=1,
∴PM=3-x,
∴PF2=PM2+MF2,
∴y2=![]() ,
,
利用描点法作出图象,如图所示:
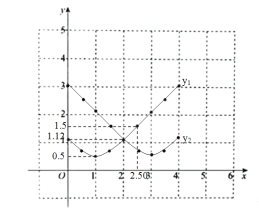
(3)如上图;
①由图象可得:函数y1的最小值是0.5;
②答案不唯一,如,如:用几何背景意义可知:函数y1的图象与函数y2的图象的交点表示的含义是:当PE=PF=1.12cm时,由图象可得:AP的长为2cm;
③∵PC=AC-AP=4-x,
∵PE=PC,
∴y1=4-x,
利用图象可得:x=2.50.
故答案为①0.5;②当PE=PF=1.12cm时,AP的长为2cm;③2.50.

【题目】当今,人们对健康愈加重视,跑步锻炼成了人们的首要选择,许多与运动有关的手机APP应运而生,聪聪给自己定了目标,每天跑步![]() 公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
日期 | 18日 | 19日 | 20日 | 21日 | 22日 | 23日 | 24日 |
路程(公里) | +1.72 | +3.20 | —1.91 | —0.96 | —1.88 | +3.30 | +0.07 |
(1)分别用含![]() 的代数式表示22日及23日的跑步路程;
的代数式表示22日及23日的跑步路程;
(2)如图所示是聪聪24日跑步路程是7.07公里,求![]() 的值;
的值;
(3)若跑步一公里消耗的热量为60千卡,请问聪聪跑步七天一共消耗了多少热量?