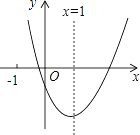题目内容
【题目】一个三位数，十位上的数字是百位上数字的2倍，十位上的数字比个位上的数字大1.
（1）若设百位上的数字为a，则个位数字为 ，这个三位数可表示为 ；
（2）这个三位数能被5整除吗？若能，求出这个三位数；若不能请说明理由.
【答案】（1）
，
（2）能，这个三位数为365.
【解析】
试题（1）用字母表示各数位的数，在写这个三位数时，百位上的字母要乘以100，十位上要乘以10；（2）能被5整除的数的特点是：个位数要么是5，要么是0.
试题解析：（1）设百位上的数字为a ，所以十位上的数字是2 a，又因为十位上的数字比个位上的数字大1，所以个位数字为
；所以这个三位数为：
；（2）这个三位数如果能被5整除，则个位数必须是5或0，若
，则
，a是分数，不符合实际要求. 若
，则a=3，这时这个三位数是365.
灵星计算小达人系列答案
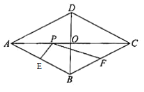
孟建平错题本系列答案
【题目】如图，在菱形ABCD中，对角线AC，相交于点O，
cm，
cm，E，F分别是AB，BC的中点，点P是对角线AC上的一个动点，设
cm，
cm，
cm
小明根据学习函数的经验，分别对这两种函数随自变量的变化而变化的情况进行了探究，下面是小明探究过程，请补充完整：
（1）画函数
的图象
①按下表自变量的值进行取点、画图、测量，得到了与x的几组对应值：
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
| 1.12 | 0.5 | 0.71 | 1.12 | 1.58 | 2.06 | 2.55 | 3.04 |
②在所给坐标系中描出补全后的表中的各对应值为坐标的点，画出函数的图象；
（2）画函数
的图象
在同一坐标系中，画出函数的图象；
（3）根据画出的函数的图象、函数的图象，解决问题
①函数的最小值是________________；
②函数的图象与函数的图象的交点表示的含义是________________；
③若
，AP的长约为________________cm
