题目内容
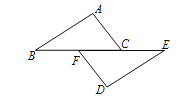
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②AF
∥EB;③∠FAN=∠EAM;④△ACN≌△ABM![]() 其中正确的有 .
其中正确的有 .
【答案】![]()
【解析】由∠E=∠F=90°,∠B=∠C,AE=AF,利用“AAS”得到△ABE与△ACF全等,根据全等三角形的对应边相等且对应角相等即可得到∠EAB与∠FAC相等,AE与AF相等,AB与AC相等,然后在等式∠EAB=∠FAC两边都减去∠MAN,得到∠EAM与∠FAN相等,然后再由∠E=∠F=90°,AE=AF,∠EAM=∠FAN,利用“ASA”得到△AEM与△AFN全等,利用全等三角形的对应边相等,对应角相等得到选项①和③正确;然后再∠C=∠B,AC=AB,∠CAN=∠BAM,利用“ASA”得到△ACN与△ABM全等,故选项④正确;若选项②正确,得到∠F与∠BDN相等,且都为90°,而∠BDN不一定为90°,故②错误.
解:在△ABE和△ACF中,
∠E=∠F=90°,AE=AF,∠B=∠C,
∴△ABE≌△ACF,
∴∠EAB=∠FAC,AE=AF,AB=AC,
∴∠EAB-∠MAN=∠FAC-∠NAM,即∠EAM=∠FAN,
在△AEM和△AFN中,
∠E=∠F=90°,AE=AF,∠EAM=∠FAN,
∴△AEM≌△AFN,
∴EM=FN,∠FAN=∠EAM,故选项①和③正确;
在△ACN和△ABM中,
∠C=∠B,AC=AB,∠CAN=∠BAM(公共角),
∴△ACN≌△ABM,故选项④正确;
若AF∥EB,∠F=∠BDN=90°,而∠BDN不一定为90°,故②错误,
则正确的选项有:①③④.
故答案为:①③④

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目