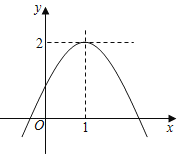ĢāÄæÄŚČŻ
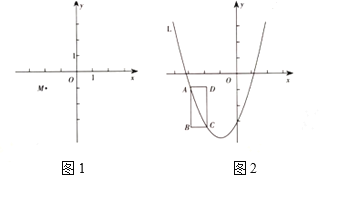
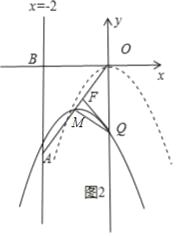
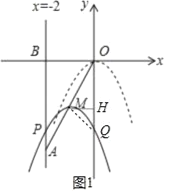
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖµćA(©2£¬©4)£¬Ö±Ļßx=©2ÓėxÖįĻą½»ÓŚµćB£¬Į¬½ÓOA£¬Å×ĪļĻßy=©x2“ÓµćOŃŲOA·½ĻņĘ½ŅĘ£¬ÓėÖ±Ļßx=©2½»ÓŚµćP£¬¶„µćMµ½µćAŹ±Ķ£Ö¹ŅĘ¶Æ£®
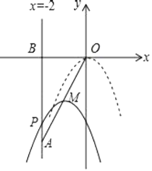
£Ø1£©Ļ߶ĪOAĖłŌŚÖ±ĻßµÄŗÆŹż½āĪöŹ½ŹĒ”” £»
£Ø2£©ÉčĘ½ŅĘŗóÅ×ĪļĻߵĶ„µćMµÄŗį×ų±źĪŖm£¬ĪŹ£ŗµ±mĪŖŗĪÖµŹ±£¬Ļ߶ĪPA×ī³¤£æ²¢Ēó³ö“ĖŹ±PAµÄ³¤£®
£Ø3£©ČōĘ½ŅĘŗóÅ×ĪļĻß½»yÖįÓŚµćQ£¬ŹĒ·ń“ęŌŚµćQŹ¹µĆ”÷OMQĪŖµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³öµćQµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y=2x£»£Ø2£©µ±m=1Ź±£¬PAµÄÖµ×ī“ó£¬PAµÄ×ī“óÖµĪŖ1£»£Ø3£©“ęŌŚ£¬(0£¬5©2![]() )»ņ(0£¬©8)
)»ņ(0£¬©8)
”¾½āĪö”æ
£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·ØĒóÖ±ĻßOAµÄ½āĪöŹ½£»
£Ø2£©ÉčMµćµÄ×ų±źĪŖ£Øm£¬2m£©£¬£Ø©2”Üm£¼0£©£¬ĄūÓƶ„µćŹ½Š“³öĘ½ŅĘŗóÅ×ĪļĻß½āĪöŹ½ĪŖy=©£Øx©m£©2+2m£¬Ōņ PµćµÄ×ų±źĪŖ£Ø©2£¬©m2©2m©4£©£¬ĖłŅŌPA=©m2©2m£¬Č»ŗóĄūÓƶž“ĪŗÆŹżµÄŠŌÖŹ½ā¾öĪŹĢā£»
£Ø3£©ĻČČ·¶ØOQ=m2©2m£¬OM=©![]() m£¬ŌŁĢÖĀŪ£ŗµ±OM=OQ£¬¼“©
m£¬ŌŁĢÖĀŪ£ŗµ±OM=OQ£¬¼“©![]() m=m2©2m£¬Č»ŗó½ā·½³ĢĒó³öm¼“æɵƵ½“ĖŹ±Qµć×ų±ź£»µ±OM=MQ£¬×÷MH”ĶOQÓŚH£¬ČēĶ¼1£¬ĄūÓĆOH=QHµĆµ½©2m=m2©2m©£Ø©2m£©£¬Č»ŗó½ā·½³ĢĒó³öm¼“æɵƵ½Qµć×ų±ź£»µ±QM=QO£¬×÷QF”ĶOMÓŚF£¬ČēĶ¼2£¬ŌņOF=MF=©
m=m2©2m£¬Č»ŗó½ā·½³ĢĒó³öm¼“æɵƵ½“ĖŹ±Qµć×ų±ź£»µ±OM=MQ£¬×÷MH”ĶOQÓŚH£¬ČēĶ¼1£¬ĄūÓĆOH=QHµĆµ½©2m=m2©2m©£Ø©2m£©£¬Č»ŗó½ā·½³ĢĒó³öm¼“æɵƵ½Qµć×ų±ź£»µ±QM=QO£¬×÷QF”ĶOMÓŚF£¬ČēĶ¼2£¬ŌņOF=MF=©![]() m£¬Ö¤Ć÷Rt”÷OFQ”×Rt”÷ABO£¬ĄūÓĆĻąĖʱȵƵ½
m£¬Ö¤Ć÷Rt”÷OFQ”×Rt”÷ABO£¬ĄūÓĆĻąĖʱȵƵ½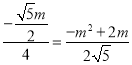 £¬½āµĆm²»Āś×ćĢõ¼žÉįČ„£®
£¬½āµĆm²»Āś×ćĢõ¼žÉįČ„£®
½ā£ŗ£Ø1£©ÉčÖ±ĻßOAµÄ½āĪöŹ½ĪŖy=kx£¬
°Ń£Ø©2£¬©4£©“śČėµĆ©2k=©4£¬½āµĆk=2£¬
ĖłŅŌÖ±ĻßOAµÄ½āĪöŹ½ĪŖy=2x£»
¹Ź“š°øĪŖy=2x£»
£Ø2£©ÉčMµćµÄ×ų±źĪŖ£Øm£¬2m£©£¬£Ø©2”Üm£¼0£©£¬
”ąĘ½ŅĘŗóÅ×ĪļĻß½āĪöŹ½ĪŖy=©£Øx©m£©2+2m£¬
µ±x=©2Ź±£¬y=©£Ø2©m£©2+2m=©m2©2m©4£¬
”ąPµćµÄ×ų±źĪŖ£Ø©2£¬©m2©2m©4£©£¬
”ąPA=©m2©2m©4©£Ø©4£©=©m2©2m=©£Øm©1£©2+1
”ąµ±m=1Ź±£¬PAµÄÖµ×ī“ó£¬PAµÄ×ī“óÖµĪŖ1£»
£Ø3£©“ęŌŚ£¬ĄķÓÉČēĻĀ£ŗ
µ±x=0Ź±£¬y=©£Ø0©m£©2+2m=©m2+2m£¬ŌņQ£Ø0£¬©m2+2m£©£¬
”ßOQ=m2©2m£¬OM=©![]() m£¬
m£¬
µ±OM=OQ£¬¼“©![]() m=m2©2m£¬¼“m2©£Ø2©
m=m2©2m£¬¼“m2©£Ø2©![]() £©m=0£¬½āµĆm1=0£ØÉįČ„£©£¬m2=2©
£©m=0£¬½āµĆm1=0£ØÉįČ„£©£¬m2=2©![]() £¬“ĖŹ±Qµć×ų±źĪŖ£Ø0£¬5©2
£¬“ĖŹ±Qµć×ų±źĪŖ£Ø0£¬5©2![]() £©£»
£©£»
µ±OM=MQ£¬×÷MH”ĶOQÓŚH£¬ČēĶ¼1£¬ŌņOH=QH£¬©2m=m2©2m©£Ø©2m£©£¬¼“m2+2m=0£¬½āµĆm1=0£ØÉįČ„£©£¬m2=©2£¬“ĖŹ±Qµć×ų±źĪŖ£Ø0£¬©8£©£»
µ±QM=QO£¬×÷QF”ĶOMÓŚF£¬ČēĶ¼2£¬ŌņOF=MF=©![]() m£¬
m£¬
”ßOQ”ĪAB£¬
”ą”ĻQOF=”ĻBAO£¬
”ąRt”÷OFQ”×Rt”÷ABO£¬
”ą![]() £¬¼“
£¬¼“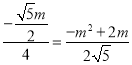 £¬ÕūĄķµĆ4m2©3m=0£¬½āµĆm1=0£ØÉįČ„£©£¬m2=
£¬ÕūĄķµĆ4m2©3m=0£¬½āµĆm1=0£ØÉįČ„£©£¬m2=![]() £ØÉįČ„£©£¬
£ØÉįČ„£©£¬
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄQµć×ų±źĪŖ£Ø0£¬5©2![]() £©»ņ£Ø0£¬©8£©£®
£©»ņ£Ø0£¬©8£©£®

 ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø
ĢģĢģĻņÉĻŅ»±¾ŗĆ¾ķĻµĮŠ“š°ø Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø
Š”ѧɜ10·ÖÖÓÓ¦ÓĆĢāĻµĮŠ“š°ø”¾ĢāÄæ”æ¼×”¢ŅŅĮ½Ćū¶ÓŌ±²Ī¼ÓÉä»÷ѵĮ·£¬³É¼Ø·Ö±š±»ÖĘ³ÉĻĀĮŠĮ½øöĶ³¼ĘĶ¼£ŗ
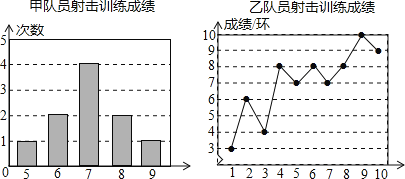
øł¾ŻŅŌÉĻŠÅĻ¢£¬ÕūĄķ·ÖĪöŹż¾ŻČēĻĀ£ŗ
Ę½¾ł³É¼Ø/»· | ÖŠĪ»Źż/»· | ÖŚŹż/»· | ·½²ī | |
¼× | a | 7 | 7 | 1.2 |
ŅŅ | 7 | b | 8 | c |
£Ø1£©Š“³ö±ķøńÖŠa£¬b£¬cµÄÖµ£ŗa£½”” ””£¬b£½”” ””£¬c£½”” ””£®
£Ø2£©Čē¹ūŅŅŌŁÉä»÷Ņ»“Ī£¬ĆüÖŠ7»·£¬ÄĒĆ“ŅŅµÄÉä»÷³É¼ØµÄ·½²ī”” ””£®£ØĢī”°±ä“ó”±”°±äŠ””±”°²»±ä”±£©
£Ø3£©½ĢĮ·øł¾ŻÕā10“Ī³É¼ØČōŃ”Ōń¼×²Ī¼Ó±ČČü£¬½ĢĮ·µÄĄķÓÉŹĒŹ²Ć“£æ