ЬтФПФкШн
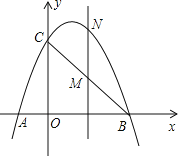
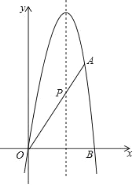
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=ax2+bxЃЈaЁй0ЃЉЙ§ЕуAЃЈ![]() ЃЌЉ3ЃЉКЭЕуBЃЈ3
ЃЌЉ3ЃЉКЭЕуBЃЈ3![]() ЃЌ0ЃЉЃЎЙ§ЕуAзїжБЯпACЁЮxжсЃЌНЛyжсгкЕуCЃЎ
ЃЌ0ЃЉЃЎЙ§ЕуAзїжБЯпACЁЮxжсЃЌНЛyжсгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЩЯШЁвЛЕуPЃЌЙ§ЕуPзїжБЯпACЕФДЙЯпЃЌДЙзуЮЊDЃЎСЌНгOAЃЌЪЙЕУвдAЃЌDЃЌPЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЧѓГіЖдгІЕуPЕФзјБъЃЛ
ЃЈ3ЃЉХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУSЁїAOC=![]() SЁїAOQЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
SЁїAOQЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
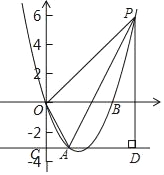
ЁОД№АИЁПЃЈ1ЃЉy=![]() x2Љ
x2Љ![]() xЃЛЃЈ2ЃЉPЕФзјБъЮЊЃЈ
xЃЛЃЈ2ЃЉPЕФзјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ4
ЃЉЛђЃЈ4![]() ЃЌ6ЃЉЛђЃЈ
ЃЌ6ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ0ЃЌ0ЃЉЃЛЃЈ3ЃЉQЃЈ3
ЃЉЛђЃЈ0ЃЌ0ЃЉЃЛЃЈ3ЃЉQЃЈ3![]() ЃЌ0ЃЉЛђЃЈЉ2
ЃЌ0ЃЉЛђЃЈЉ2![]() ЃЌ15ЃЉЃЎ
ЃЌ15ЃЉЃЎ
ЁОНтЮіЁП
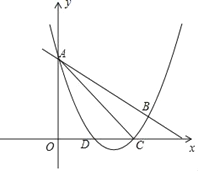
ЃЈ1ЃЉАбAгыBзјБъДњШыХзЮяЯпНтЮіЪНЧѓГіaгыbЕФжЕЃЌМДПЩШЗЖЈГіНтЮіЪНЃЛ
ЃЈ2ЃЉЩшPзјБъЮЊЃЈxЃЌ![]() x2-
x2-![]() xЃЉЃЌБэЪОГіADгыPDЃЌгЩЯрЫЦЗжСНжжЧщПіЕУБШР§ЧѓГіxЕФжЕЃЌМДПЩШЗЖЈГіPзјБъЃЛ
xЃЉЃЌБэЪОГіADгыPDЃЌгЩЯрЫЦЗжСНжжЧщПіЕУБШР§ЧѓГіxЕФжЕЃЌМДПЩШЗЖЈГіPзјБъЃЛ
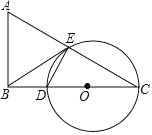
ЃЈ3ЃЉДцдкЃЌЧѓГівбжЊШ§НЧаЮAOCБпOAЩЯЕФИпhЃЌЙ§OзїOMЁЭOAЃЌНиШЁOM=hЃЌгыyжсНЛгкЕуNЃЌЗжБ№ШЗЖЈГіMгыNзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпMNНтЮіЪНЃЌгыХзЮяЯпНтЮіЪНСЊСЂЧѓГіQзјБъМДПЩЃЎ
ЃЈ1ЃЉАбAЃЈ![]() ЃЌЉ3ЃЉКЭЕуBЃЈ3
ЃЌЉ3ЃЉКЭЕуBЃЈ3![]() ЃЌ0ЃЉДњШыХзЮяЯпЕУЃК
ЃЌ0ЃЉДњШыХзЮяЯпЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКa=![]() ЃЌb=Љ
ЃЌb=Љ![]() ЃЌ
ЃЌ
дђХзЮяЯпНтЮіЪНЮЊy=![]() x2Љ
x2Љ![]() xЃЛ
xЃЛ
ЃЈ2ЃЉЕБPдкжБЯпADЩЯЗНЪБЃЌ
ЩшPзјБъЮЊЃЈxЃЌ![]() x2Љ
x2Љ![]() xЃЉЃЌдђгаAD=xЉ
xЃЉЃЌдђгаAD=xЉ![]() ЃЌPD=
ЃЌPD=![]() x2Љ
x2Љ![]() x+3ЃЌ
x+3ЃЌ
ЕБЁїOCAЁзЁїADPЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ећРэЕУЃК3x2Љ9![]() x+18=2
x+18=2![]() xЉ6ЃЌМД3x2Љ11
xЉ6ЃЌМД3x2Љ11![]() x+24=0ЃЌ
x+24=0ЃЌ
НтЕУЃКx=![]() ЃЌМДx=
ЃЌМДx=![]() Лђx=
Лђx=![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ДЫЪБPЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛ
ЃЉЃЛ
ЕБЁїOCAЁзЁїPDAЪБЃЌ![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
ећРэЕУЃК![]() x2Љ9x+6
x2Љ9x+6![]() =6xЉ6
=6xЉ6![]() ЃЌМДx2Љ5
ЃЌМДx2Љ5![]() x+12=0ЃЌ
x+12=0ЃЌ
НтЕУЃКx=![]() ЃЌМДx=4
ЃЌМДx=4![]() Лђ
Лђ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
ДЫЪБPЃЈ4![]() ЃЌ6ЃЉЃЛ
ЃЌ6ЃЉЃЛ
ЕБЕуPЃЈ0ЃЌ0ЃЉЪБЃЌвВТњзуЁїOCAЁзЁїPDAЃЛ
ЕБPдкжБЯпADЯТЗНЪБЃЌЭЌРэПЩЕУЃКPЕФзјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
злЩЯЃЌPЕФзјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ4
ЃЉЛђЃЈ4![]() ЃЌ6ЃЉЛђЃЈ
ЃЌ6ЃЉЛђЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЛђЃЈ0ЃЌ0ЃЉЃЛ
ЃЉЛђЃЈ0ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉдкRtЁїAOCжаЃЌOC=3ЃЌAC=![]() ЃЌ
ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃКOA=2![]() ЃЌ
ЃЌ
Ёп![]() OCAC=
OCAC=![]() OAhЃЌ
OAhЃЌ
Ёрh=![]() ЃЌ
ЃЌ
ЁпSЁїAOC=![]() SЁїAOQ=
SЁїAOQ=![]() ЃЌ
ЃЌ
ЁрЁїAOQБпOAЩЯЕФИпЮЊ![]() ЃЌ
ЃЌ
Й§OзїOMЁЭOAЃЌНиШЁOM=![]() ЃЌЙ§MзїMNЁЮOAЃЌНЛyжсгкЕуNЃЌШчЭМЫљЪОЃК
ЃЌЙ§MзїMNЁЮOAЃЌНЛyжсгкЕуNЃЌШчЭМЫљЪОЃК

дкRtЁїOMNжаЃЌON=2OM=9ЃЌМДNЃЈ0ЃЌ9ЃЉЃЌ
Й§MзїMHЁЭxжсЃЌ
дкRtЁїOMHжаЃЌMH=![]() OM=
OM=![]() ЃЌOH=
ЃЌOH=![]() OM=
OM=![]() ЃЌМДMЃЈ
ЃЌМДMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшжБЯпMNНтЮіЪНЮЊy=kx+9ЃЌ
АбMзјБъДњШыЕУЃК![]() =
=![]() k+9ЃЌМДk=Љ
k+9ЃЌМДk=Љ![]() ЃЌМДy=Љ
ЃЌМДy=Љ![]() x+9ЃЌ
x+9ЃЌ
СЊСЂЕУЃК ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]() ЃЌМДQЃЈ3
ЃЌМДQЃЈ3![]() ЃЌ0ЃЉЛђЃЈЉ2
ЃЌ0ЃЉЛђЃЈЉ2![]() ЃЌ15ЃЉЃЌ
ЃЌ15ЃЉЃЌ
дђХзЮяЯпЩЯДцдкЕуQЃЌЪЙЕУSЁїAOC=![]() SЁїAOQЃЌДЫЪБЕуQЕФзјБъЮЊЃЈ3
SЁїAOQЃЌДЫЪБЕуQЕФзјБъЮЊЃЈ3![]() ЃЌ0ЃЉЛђЃЈЉ2
ЃЌ0ЃЉЛђЃЈЉ2![]() ЃЌ15ЃЉЃЎ
ЃЌ15ЃЉЃЎ