题目内容
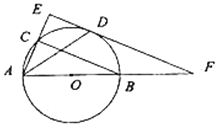
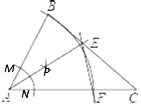
【题目】如图,在△ABC中,∠ABC=2∠C,小明做了如下操作:
(Ⅰ)以A为圆心,AB长为半径画弧,交AC于点F;
(Ⅱ)以A为圆心,任意长为半径画弧,交AB、AC于M、N两点,分别以M、N为圆心,以大于![]() MN为半径画弧,两弧交于一点P,作射线AP,交BC于点E;
MN为半径画弧,两弧交于一点P,作射线AP,交BC于点E;
(Ⅲ)作直线EF.
依据小明尺规作图的方法,若AB=3.3,BE=1.8,则AC的长为___________;
【答案】5.1
【解析】
根据题意的尺规作图可知AE是∠BAC的角平分线,再根据等腰三角形的性质及外角定理进行求解.
根据题意的尺规作图可知AE是∠BAC的角平分线,△ABE≌△AFE
∵∠ABC=2∠C,
∴∠C=∠EAC,故AE=CE,
又AE=AF,∴∠AEF=∠AFE,
根据外角定理得∠BEA=∠C+∠EAC,∠AFE=∠C+∠FEC,
∴∠EAC=∠C=∠FEC,故EF=FC,
∴AC=AF+FC=AB+BE=5.1

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目