题目内容
【题目】某商店经营一种文化衫,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件文化衫售价不能高于40元.设每件文化衫的销售单价上涨了![]() 元时(
元时(![]() 为正整数),月销售利润为
为正整数),月销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围.
的取值范围.
(2)每件文化衫的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
【答案】(1)![]() ;自变量x的取值范围是:
;自变量x的取值范围是:![]() (
(![]() 也正确)且
也正确)且![]() 为正整数;(2)每件文化衫的售价定为36元或37元时,每个月可获得最大利润.最大的月利润是2720元.
为正整数;(2)每件文化衫的售价定为36元或37元时,每个月可获得最大利润.最大的月利润是2720元.
【解析】
(1)根据题意知一件文化衫的利润为(30+x-20)元,月销售量为(230-10x),然后根据月销售利润=一件玩具的利润×月销售量即可求出函数关系式.
(2)把y=-10x2+130x+2300化成顶点式,求得当x=6.5时,y有最大值,再根据0<x≤10且x为正整数,分别计算出当x=6和x=7时y的值即可.
(1)依题意得![]() ;
;
自变量x的取值范围是:![]() (
(![]() 也正确)且
也正确)且![]() 为正整数,
为正整数,
(2)![]() ,
,
![]()
![]() 当
当![]() 时,y有最大值.
时,y有最大值.
![]() (
(![]() 也正确)且
也正确)且![]() 为正整数
为正整数
![]() 当
当![]() 时,
时,![]() ,
,![]() (元) 当
(元) 当![]() 时,
时,![]() ,
,![]() (元)
(元)
所以,每件文化衫的售价定为36元或37元时,每个月可获得最大利润.最大的月利润是2720元.

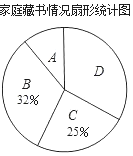
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.