��Ŀ����
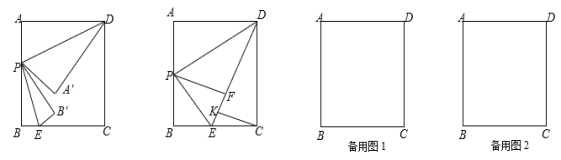
����Ŀ����֪��������A��B��C���㣬�ֱ��ʾ��������26����10��10������P��A��������ÿ��1����λ���ٶ����յ�C�ƶ������P�ƶ�ʱ��Ϊt�룮
��1���ú�t�Ĵ���ʽ��ʾP���Ӧ������__________��
�ú�t�Ĵ���ʽ��ʾ��P�͵�C�ľ��룺PC=_____________.
��2������P�˶���B��ʱ����Q��A���������ÿ��3����λ���ٶ���C���˶���Q�㵽��C�����������ͬ�����ٶȷ��ص�A��
�ٵ�P��Qͬʱ�˶��˶��Ĺ�������__________������������ʱt=_______________�룮
���ڵ�Q��ʼ�˶�������t�Ĵ���ʽ��ʾP��Q�����ľ��룮���������ѣ�ע�⿼��P��Q��λ�ã�
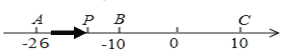
���𰸡���1����26+t��36��t��
��2��2����24���30�룻
��3����16��t��24ʱ PQ=��2t+48��
��24��t��28ʱ PQ=2t-48��
��28��t��30ʱ PQ= 120��4t��
��30��t��36ʱ PQ= 4t��120
����������1�����������ľ��룬�ɵ�P����A�͵�C�ľ��룻
��2�����������ľ��룬Ҫ��t�������ۣ�t��ͬ��Χ���ɵò�ͬPQ��
�⣺��1��P���Ӧ����Ϊ��26+t��PC=36��t��
�ʴ�Ϊ����26+t��36��t��
��2������2��������
�����������
Q����ǰ������3��t��16��=t��
��ã�t=24��
Q���غ�������3��t��16��+t=36��2��
��ã�t=30��
��������������ʱt=24���30�룮
�ʴ�Ϊ�� 24��30��
�ڵ�16��t��24ʱ��PQ=t��3��t��16��=��2t+48��
��24��t��28ʱ��PQ=3��t��16����t=2t��48��
��28��t��30ʱ��PQ=72��3��t��16����t=120��4t��
��30��t��36ʱ��PQ=t��[72��3��t��16��]=4t��120��
��36��t��40ʱ��PQ=3��t��16����36=3t-84��
���㾦�����⿼�������ᣬһԪһ�η��̵�Ӧ�ã����2������Ҫ��t���������ǽ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�