题目内容
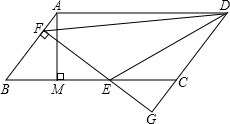 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连接DE、DF.有下面三个结论:
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连接DE、DF.有下面三个结论:(1)△BEF∽△CEG;
(2)当点E在线段BC上运动时,△BEF和△CEG的周长之和为24;
(3)当BE=
| 55 |
| 6 |
| 121 |
| 6 |
其中正确结论的序号是
(1)(2)(3)
(1)(2)(3)
.分析:(1)由AB∥DG,即可直接得到两个三角形相似.
(2)利用勾股定理可求出BM=3,又因为Rt△BEF∽Rt△BAM,令BE=x,那么根据相似比,可用含x的代数式分别表示EF,BF,同样在△CEG中,令CE=y,可用含y的代数式表示CG,EG,又x+y=10,那么能求出两三角形的周长和是
(x+y)=24.
(3)利用相似比、勾股定理可得EF=
x,CG=
(10-x),那么利用三角形的面积公式,可得到y与x的关系式,再根据二次函数求最大值来求即可.
(2)利用勾股定理可求出BM=3,又因为Rt△BEF∽Rt△BAM,令BE=x,那么根据相似比,可用含x的代数式分别表示EF,BF,同样在△CEG中,令CE=y,可用含y的代数式表示CG,EG,又x+y=10,那么能求出两三角形的周长和是
| 12 |
| 5 |
(3)利用相似比、勾股定理可得EF=
| 4 |
| 5 |
| 3 |
| 5 |
解答:解:(1)∵四边形ABCD是平行四边形,∴AB∥DG,
∴∠B=∠GCE,∠G=∠BFE,
∴△BEF∽△CEG,故此选项正确;
(2)过点C作FG的平行线交直线AB于H,
因为GF⊥AB,所以四边形FHCG为矩形.
所以FH=CG,FG=CH,
因此,△BEF与△CEG的周长之和等于BC+CH+BH,
∵∠B=∠B,∠AMB=∠BHC=90°
∴△ABM∽△CBH,
∴
=
由BC=10,AB=5,AM=4,
可得CH=8,
∴BH=6,
所以BC+CH+BH=24,故此选项正确;
(3)设BE=x,则EF=
x,GC=
(10-x),
所以y=
EF•DG=
•
x[
(10-x)+5]=-
x2+
x,
配方得:y=-
(x-
)2+
.
所以,当x=
时,y有最大值.
最大值为
,故此选项正确.
故答案为:(1)(2)(3).
∴∠B=∠GCE,∠G=∠BFE,

∴△BEF∽△CEG,故此选项正确;
(2)过点C作FG的平行线交直线AB于H,
因为GF⊥AB,所以四边形FHCG为矩形.
所以FH=CG,FG=CH,
因此,△BEF与△CEG的周长之和等于BC+CH+BH,
∵∠B=∠B,∠AMB=∠BHC=90°
∴△ABM∽△CBH,
∴
| AB |
| BC |
| AM |
| CH |
由BC=10,AB=5,AM=4,
可得CH=8,
∴BH=6,
所以BC+CH+BH=24,故此选项正确;
(3)设BE=x,则EF=
| 4 |
| 5 |
| 3 |
| 5 |
所以y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
| 6 |
| 25 |
| 22 |
| 5 |
配方得:y=-
| 6 |
| 25 |
| 55 |
| 6 |
| 121 |
| 6 |
所以,当x=
| 55 |
| 6 |
最大值为
| 121 |
| 6 |
故答案为:(1)(2)(3).
点评:此题主要考查了相似三角形的判定和性质,勾股定理,三角形的面积公式,二次函数求最大值的问题,熟练掌握相似三角形的判定与性质是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 次方程x2-7x+12=0的两个根,且OA>OB.
次方程x2-7x+12=0的两个根,且OA>OB. 10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是
10、如图,平行四边形ABCD中,∠ABC的角平分线BE交AD于E点,AB=3,ED=1,则平行四边形ABCD的周长是

 如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是
如图,平行四边形ABCD中,对角线AC和BD相交于点O,如果AC=12,BD=10,AB=m,那么m的取值范围是 如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为
如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,DB=8,则四边形ABCD是的周长为