题目内容
【题目】某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的![]() 倍,且每天包装大黄米和江米的质量之和为45千克.
倍,且每天包装大黄米和江米的质量之和为45千克.
(1)求平均每天包装大黄米和江米的质量各是多少千克?
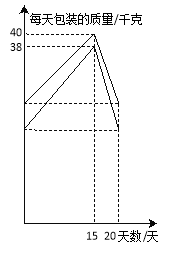
(2)为迎接今年6月20日的“端午节”,该超市决定在节日前20天增加每天包装大黄米和江米的质量,二者的包装质量与天数的变化情况如图所示,节日后又恢复到原来每天的包装质量.分别求出在这20天内每天包装大黄米和江米的质量随天数变化的函数关系式,并写出自变量的取值范围.
(3)假设该超市每天都会将当天包装后的大黄米和江米全部出售,已知大黄米成本价为每千克7.9元,江米成本价为每千克9.5元,二者包装费用平均每千克均为0.5元,大黄米售价为每千克10元,江米售价为每千克12元,那么在这20天中有哪几天销售大黄米和江米的利润之和大于120元? [总利润=售价额-成本-包装费用]
【答案】(1)大黄米25千克,江米20千克.(2)![]() (
(![]() ),
),![]() (
(![]() ),
),![]() (
(![]() ),
), ![]() (
(![]() ),(3)第11,12,13,14,15,16天中销售大黄米和江米的总利润大于120元.
),(3)第11,12,13,14,15,16天中销售大黄米和江米的总利润大于120元.
【解析】
试题分析:(1)设两个未知数,由题意建立二元一次方程组求解;(2)先理解图像的意义:上面的折线是每天包装大黄米的质量随天数变化的函数图像,下面的折线是每天包装江米的质量随天数变化的函数图像,其中点(0,25),(0,20)中纵坐标分别表示原来每天大黄米和江米的包装质量.点(20,25),(20,20)纵坐标表示节日后又恢复到原来每天的包装质量.根据函数自变量取值,每段函数都代入两点坐标求出4个解析式;(3)因为总利润=大黄米每千克利润×所售千克数+江米每千克利润×所售千克数,所以设总利润为W元,则![]() ,当
,当![]() 与当
与当![]() 时建立W与x之间的函数关系式,当W大于120元时讨论x的取值,从而确定在这20天中有哪几天销售大黄米和江米的利润之和大于120元.
时建立W与x之间的函数关系式,当W大于120元时讨论x的取值,从而确定在这20天中有哪几天销售大黄米和江米的利润之和大于120元.
试题解析:(1)建立二元一次方程组,设平均每天包装大黄米和江米的质量分别为a千克和b千克,则 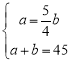 ,解得
,解得![]() .∴平均每天包装大黄米和江米的质量分别为25千克和20千克;(2)观察图象,可设平均每天包装大黄米的质量与天数的关系式为
.∴平均每天包装大黄米和江米的质量分别为25千克和20千克;(2)观察图象,可设平均每天包装大黄米的质量与天数的关系式为![]() ,平均每天包装江米的质量与天数的关系式为
,平均每天包装江米的质量与天数的关系式为![]() .①当
.①当![]() 时,由题意
时,由题意![]() 的图象过点
的图象过点![]() ,
,![]() .则可列方程组为
.则可列方程组为![]() ,解得
,解得![]() ,∴
,∴![]() .由题意
.由题意![]() 的图象过点
的图象过点![]() ,
,![]() .则可列方程组为
.则可列方程组为![]() ,解得
,解得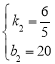 ,∴
,∴![]() .②当
.②当![]() 时,由题意
时,由题意![]() 的图象过点
的图象过点![]() ,
,![]() .则可列方程组为
.则可列方程组为![]() ,解得
,解得![]() ,∴
,∴![]() .由题意
.由题意![]() 的图象过点
的图象过点![]() ,
,![]() .则可列方程组为
.则可列方程组为![]() ,解得
,解得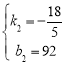 ,∴
,∴![]() .
.
∴![]() ,
, 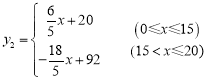 ;(3)①当
;(3)①当![]() 时,
时,![]()
![]()
![]()
![]() ,由题意得:
,由题意得:![]() ,∴
,∴![]() ,∴x的取值范围为
,∴x的取值范围为![]() ,由题意知
,由题意知![]() .②当
.②当![]() 时,
时,
![]()
![]()
![]()
![]() .由题意得:
.由题意得:![]() ,∴
,∴![]() ,∴x的取值范围为
,∴x的取值范围为![]() .由题意知
.由题意知![]() .∴由①、②可知在第11,12,13,14,15,16天中销售大黄米和江米的总利润大于120元.
.∴由①、②可知在第11,12,13,14,15,16天中销售大黄米和江米的总利润大于120元.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案