题目内容
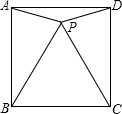
如图,已知P是边长为a的正方形ABCD内一点,△PBC是等边三角形,则△PAD的外接圆半径是( )
| A.a | B.
| C.
| D.
|

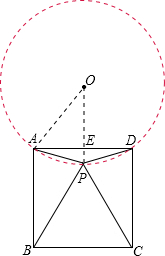
如图,设△PAD的外接圆为⊙O,
∵四边形ABCD是正方形,
∴AB=CD,
∵△PBC是等边三角形,
∴BP=CP,∠PBC=∠PCB=60°,
∴∠ABP=∠PCD=30°,
∴△ABP≌△CDP,
∴PA=PD,
∴∠APD=150°,
连接OP交AD于E点,
根据垂径定理的推论知道E为AD的中点,并且OP⊥AD,
∴∠APO=75°
而OA=OP,
∴∠AOE=30°,
∴AE=
| 1 |
| 2 |
∴AD=AE=a,
∴正方形的边长为a.
故选A.

练习册系列答案
相关题目
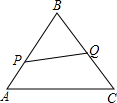 匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q运动到点C时,P,Q都停止运动.
匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q运动到点C时,P,Q都停止运动.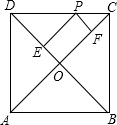 如图,已知P是边长为2的正方形ABCD的边CD任意一点,且PE⊥DB,垂足为E,PF⊥CA垂足为F,则PE+PF的长是
如图,已知P是边长为2的正方形ABCD的边CD任意一点,且PE⊥DB,垂足为E,PF⊥CA垂足为F,则PE+PF的长是 的坐标为(-1,0).
的坐标为(-1,0).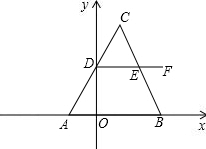 A的坐标为(-1,0).
A的坐标为(-1,0). 如图,已知△ABC是边长为2
如图,已知△ABC是边长为2