Question

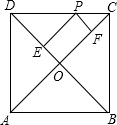如图，已知P是边长为2的正方形ABCD的边CD任意一点，且PE⊥DB，垂足为E，PF⊥CA垂足为F，则PE+PF的长是

 

．

Answer 1

分析：根据正方形的性质易知：△DOC、△DEP、△CFP都是等腰直角三角形，那么DO=OC=

2

，PE=DE；易证得四边形PFOE是矩形，则PF=OE，那么PE+PF=DE+OE=DO，由此得解．

解答：解：∵四边形ABCD是正方形，
∴DO⊥OC，且∠ODC=∠OCD=45°，
∴△DOC、△PDE、△PFC都是等腰直角三角形，
∴DO=OC=

2

，PE=DE；
∵∠PEO=∠PFO=∠EOF=90°，
∴四边形PEOF是矩形，则PF=OE；
∴PE+PF=DE+OE=DO=

2

．
故填：

2

．

点评：要擅于利用边的关系进行转化．能够发现PE+PF同正方形对角线的关系是解答此题的关键．