题目内容
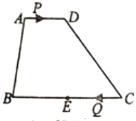
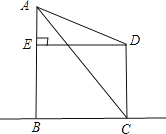
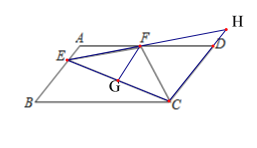
【题目】如图,在![]() ABCD中,AD=2AB,
ABCD中,AD=2AB,![]() ,垂足
,垂足![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,
,![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() :③
:③![]() ;④
;④![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由点F是AD的中点,结合![]() ABCD的性质,得FD=CD,即可判断①;先证AEFDHF,再证ECH是直角三角形,即可判断②;由EF=HF,得
ABCD的性质,得FD=CD,即可判断①;先证AEFDHF,再证ECH是直角三角形,即可判断②;由EF=HF,得![]() ,由
,由![]() ,CE⊥CD,结合三角形的面积公式,即可判断③;设∠AEF=x,则∠H=x,根据直角三角形的性质,得∠FCH=∠H=x,由FD=CD,∠DFC=∠FCH=x,由FG∥CD∥AB,得∠AEF=∠EFG=x,由EF=CF,∠EFG=∠CFG=x,进而得到
,CE⊥CD,结合三角形的面积公式,即可判断③;设∠AEF=x,则∠H=x,根据直角三角形的性质,得∠FCH=∠H=x,由FD=CD,∠DFC=∠FCH=x,由FG∥CD∥AB,得∠AEF=∠EFG=x,由EF=CF,∠EFG=∠CFG=x,进而得到![]() ,即可判断④.
,即可判断④.
∵点F是AD的中点,
∴2FD=AD,
∵在![]() ABCD中,AD=2AB,
ABCD中,AD=2AB,
∴FD=AB=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠BCF,
∴∠DCF=∠BCF,即:![]() ,
,
∴①正确;
∵AB∥CD,
∴∠A=∠FDH,∠AEF=∠H,
又∵AF=DF,
∴AEFDHF(AAS),
∴EF=HF,
∵![]() ,
,
∴CE⊥CD,即:ECH是直角三角形,
∴![]() =
=![]() EH,
EH,
∴②正确;
∵EF=HF,
∴![]()
∵![]() ,CE⊥CD,垂足
,CE⊥CD,垂足![]() 在线段
在线段![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴③错误;
设∠AEF=x,则∠H=x,
∵在RtECH中,CF=FH=EF,
∴∠FCH=∠H=x,
∵FD=CD,
∴∠DFC=∠FCH=x,
∵点F,G分别是EH,EC的中点,
∴FG∥CD∥AB,
∴∠AEF=∠EFG=x,
∵EF=CF,
∴∠EFG=∠CFG=x,
∴∠DFE=∠DFC+∠EFG+∠CFG=3x,
∴![]() .
.
∴④正确.
故选C.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目