题目内容
已知直线y=| 3 |
| 3 |
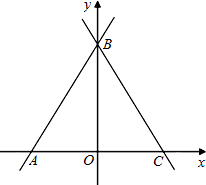 点C.
点C.(1)试确定直线BC的解析式.
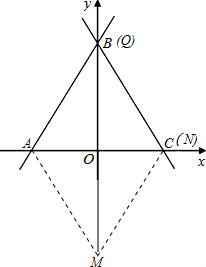
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿CBA向点A运动(不与C、A重合),动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,当△APQ的面积最大时,y轴上有一点M,平面内是否存在一点N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
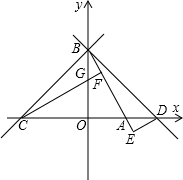
分析:(1)由已知得A点坐标,通过OA,OB长度关系,求得角BAO为60度,即能求得点C坐标,设直线BC代入BC两点即求得.
(2)当P点在AO之间运动时,作QH⊥x轴.再求得QH,从而求得三角形APQ的面积.
(3)由(2)所求可知,是存在的,写出点的坐标.
(2)当P点在AO之间运动时,作QH⊥x轴.再求得QH,从而求得三角形APQ的面积.
(3)由(2)所求可知,是存在的,写出点的坐标.
解答: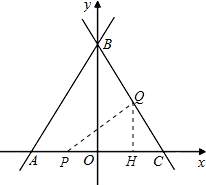 解:(1)由已知得A点坐标(-4﹐0),B点坐标(0﹐4
解:(1)由已知得A点坐标(-4﹐0),B点坐标(0﹐4
﹚,
∵OB=
OA,
∴∠BAO=60°,
∵∠ABC=60°,
∴△ABC是等边三角形,
∵OC=OA=4,
∴C点坐标﹙4,0﹚,
设直线BC解析式为y=kx﹢b,
,
∴
,
∴直线BC的解析式为y=-
x+4
;(2分)
﹙2﹚当P点在AO之间运动时,作QH⊥x轴.
∵
=
,
∴
=
,
∴QH=
t
∴S△APQ=
AP•QH=
t•
t=
t2﹙0<t≤4﹚,(2分)
同理可得S△APQ=
t•﹙8
-
t﹚=-
t2+4
t﹙4≤t<8﹚;(2分)
(3)存在,如图当Q与B重合时,四边形AMNQ为菱形,此时N坐标为(4,0)
其它类似还有(-4,8)或(-4,-8)或(-4,
).(4分)
 解:(1)由已知得A点坐标(-4﹐0),B点坐标(0﹐4
解:(1)由已知得A点坐标(-4﹐0),B点坐标(0﹐4| 3 |
∵OB=
| 3 |
∴∠BAO=60°,
∵∠ABC=60°,
∴△ABC是等边三角形,
∵OC=OA=4,
∴C点坐标﹙4,0﹚,
设直线BC解析式为y=kx﹢b,
|
∴
|

∴直线BC的解析式为y=-
| 3 |
| 3 |
﹙2﹚当P点在AO之间运动时,作QH⊥x轴.
∵
| QH |
| OB |
| CQ |
| CB |
∴
| QH | ||
4
|
| 2t |
| 8 |
∴QH=
| 3 |
∴S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
同理可得S△APQ=
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
(3)存在,如图当Q与B重合时,四边形AMNQ为菱形,此时N坐标为(4,0)
其它类似还有(-4,8)或(-4,-8)或(-4,
8
| ||
| 3 |
点评:本题考查了一次函数的运用,考查了一次函数与直线交点坐标,从而求得AB的长度,由△ABC是等边三角形,从而求得.

练习册系列答案
相关题目
 已知直线y=-3x+m和双曲线y=
已知直线y=-3x+m和双曲线y=| k |
| x |
| A、①② | B、②③ | C、③④ | D、①④ |
已知直线y=3x-2与两条坐标轴围成的三角形面积是( )
A、-
| ||
B、
| ||
C、
| ||
D、-
|
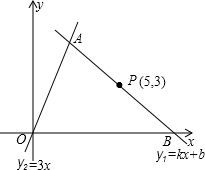 点B.设点A的横坐标为m(m>1且m≠5).
点B.设点A的横坐标为m(m>1且m≠5).