题目内容
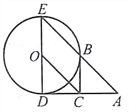
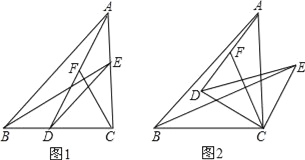
【题目】已知△ABC和△DEC都是等腰直角三角形,C为它们的公共直角顶点,D、E分别在BC、AC边上.
(1)如图1,F是线段AD上的一点,连接CF,若AF=CF;
①求证:点F是AD的中点;
②判断BE与CF的数量关系和位置关系,并说明理由;
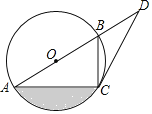
(2)如图2,把△DEC绕点C顺时针旋转α角(0<α<90°),点F是AD的中点,其他条件不变,判断BE与CF的关系是否不变?若不变,请说明理由;若要变,请求出相应的正确结论.
【答案】(1)①证明见解析;②BE=2CF,BE⊥CF;(2)仍然有BE=2CF,BE⊥CF.
【解析】
(1)①如图1,由AF=CF得到∠1=∠2,则利用等角的余角相等可得∠3=∠ADC,然后根据等腰三角形的判定定理得FD=FC,易得AF=FD;
②先利用等腰直角三角形的性质得CA=CB,CD=CE,则可证明△ADC≌△BEC得到AD=BE,∠1=∠CBE,由于AD=2CF,∠1=∠2,则BE=2CF,再证明∠CBE+∠3=90°,于是可判断CF⊥BE;
(2)延长CF到G使FG=CF,连结AG、DG,如图2,易得四边形ACDG为平行四边形,则AG=CD,AG∥CD,于是根据平行线的性质得∠GAC=180°-∠ACD,所以CD=CE=AG,再根据旋转的性质得∠BCD=α,所以∠BCE=∠DCE+∠BCD=90°+α=90°+90°-∠ACD=180°-∠ACD,得到∠GAC=∠ECB,接着可证明△AGC≌△CEB,得到CG=BE,∠2=∠1,所以BE=2CF,和前面一样可证得CF⊥BE.
(1)①证明:如图1,
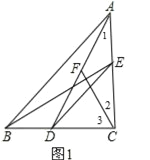
∵AF=CF,
∴∠1=∠2,
∵∠1+∠ADC=90°,∠2+∠3=90°,
∴∠3=∠ADC,
∴FD=FC,
∴AF=FD,
即点F是AD的中点;
②BE=2CF,BE⊥CF.理由如下:
∵△ABC和△DEC都是等腰直角三角形,
∴CA=CB,CD=CE,
在△ADC和△BEC中
 ,
,
∴△ADC≌△BEC,
∴AD=BE,∠1=∠CBE,
而AD=2CF,∠1=∠2,
∴BE=2CF,
而∠2+∠3=90°,
∴∠CBE+∠3=90°,
∴CF⊥BE;
(2)仍然有BE=2CF,BE⊥CF.理由如下:
延长CF到G使FG=CF,连结AG、DG,如图2,

∵AF=DF,FG=FC,
∴四边形ACDG为平行四边形,
∴AG=CD,AG∥CD,
∴∠GAC+∠ACD=180°,即∠GAC=180°﹣∠ACD,
∴CD=CE=AG,
∵△DEC绕点C顺时针旋转α角(0<α<90°),
∴∠BCD=α,
∴∠BCE=∠DCE+∠BCD=90°+α=90°+90°﹣∠ACD=180°﹣∠ACD,
∴∠GAC=∠ECB,
在△AGC和△CEB中
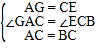 ,
,
∴△AGC≌△CEB,
∴CG=BE,∠2=∠1,
∴BE=2CF,
而∠2+∠BCF=90°,
∴∠BCF+∠1=90°,
∴CF⊥BE.
故答案为:(1)①证明见解析;②BE=2CF,BE⊥CF;(2)仍然有BE=2CF,BE⊥CF.

 名校课堂系列答案
名校课堂系列答案